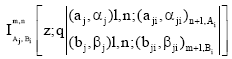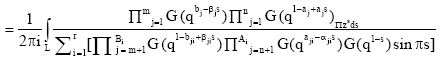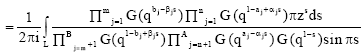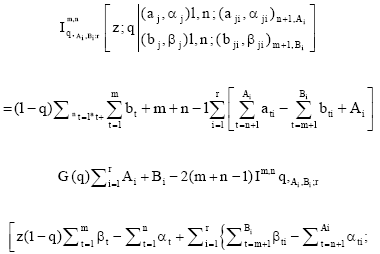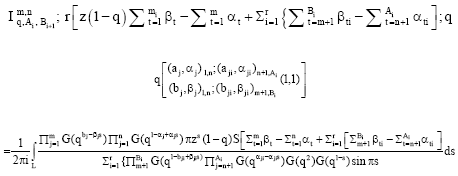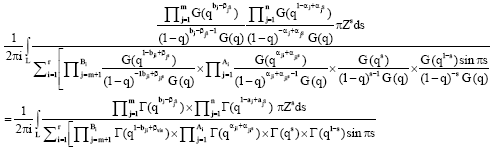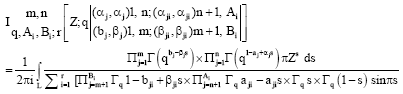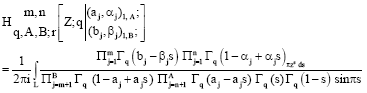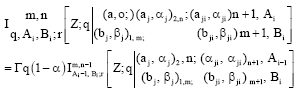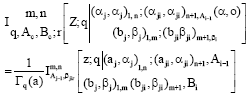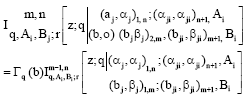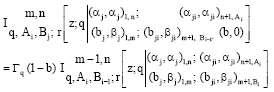Research Article
Some Transformation Formulae of Basic Analogue of I-Function
School of Mathematics and Allied Sciences, Jiwaji University, Gwalior -474 011 (M.P.), India
Renu Jain
School of Mathematics and Allied Sciences, Jiwaji University, Gwalior -474 011 (M.P.), India
D. K. Jain
Department of Applied Mathematics, Madhav Institute of Technology and Science, Gwalior-474 005 (M.P.), India