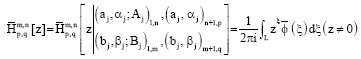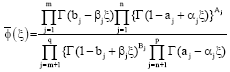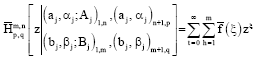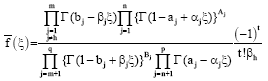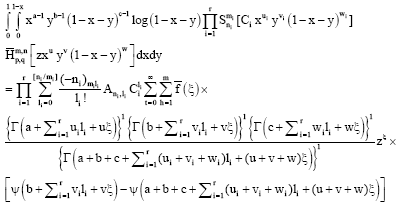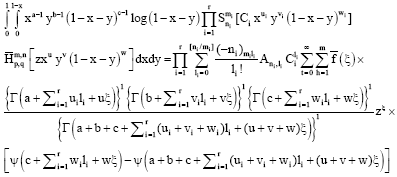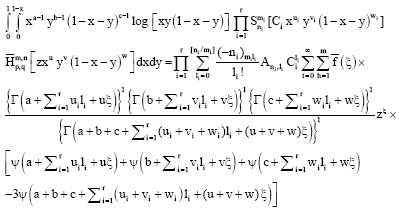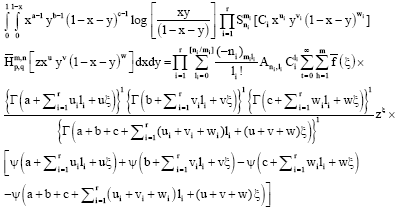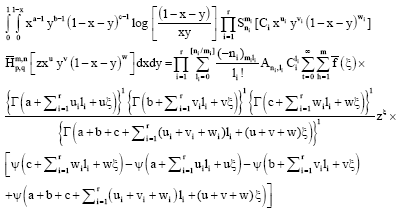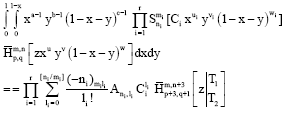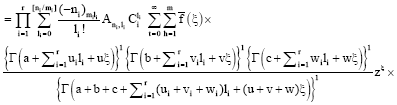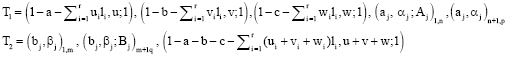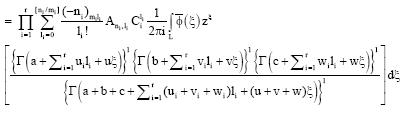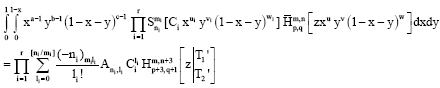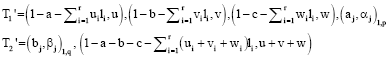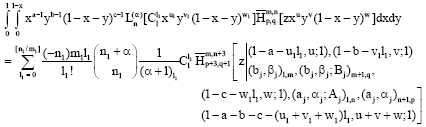Research Article
New Finite Integrals Involving Product of  -function and Srivastava Polynomial
-function and Srivastava Polynomial
Department of Mathematics, Anand International College of Engineering, Jaipur-303012, India
Mehar Chand
Department of Mathematics, Malwa College of IT and Management, Bathinda-151001, India