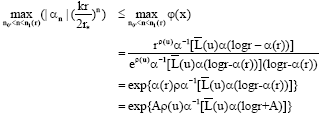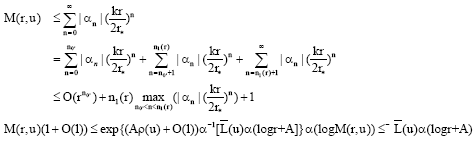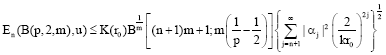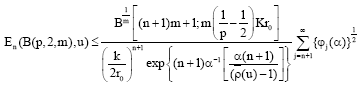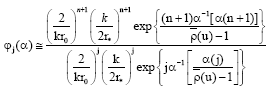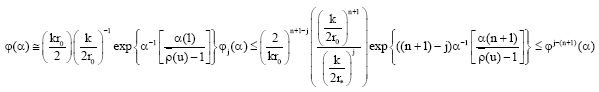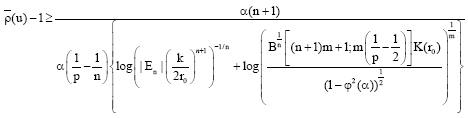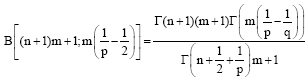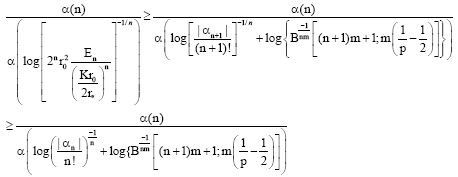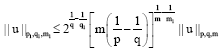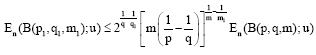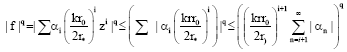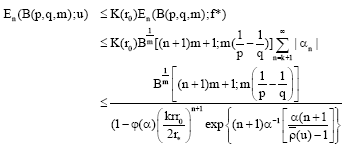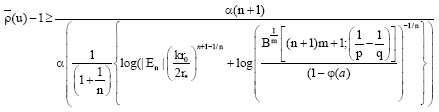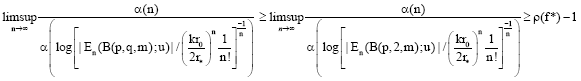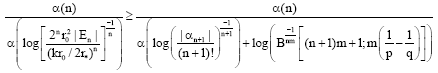Research Article
Slow Growth and Approximation of Entire Solution of Generalized Axially Symmetric Helmholtz Equation
Department of Mathematics, Aligarh Muslim University, Aligarh-202002, India
Rifaqat Ali
Department of Applied Mathematics, Aligarh Muslim University, Aligarh-202002, India