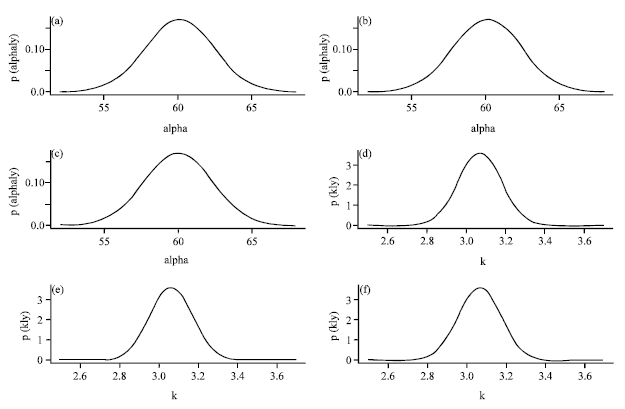
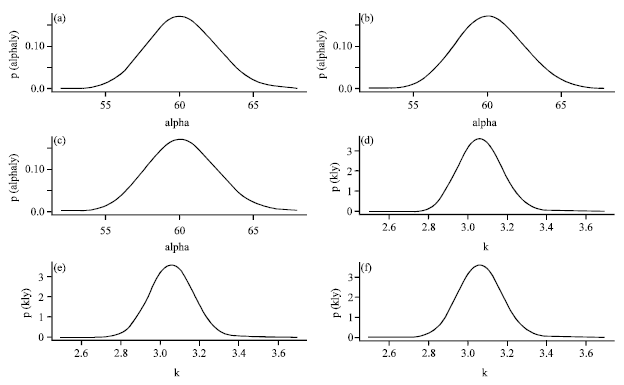
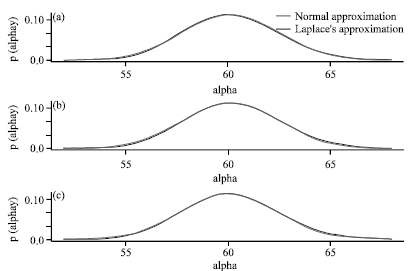
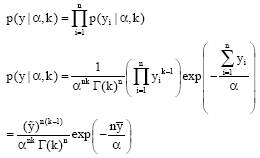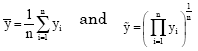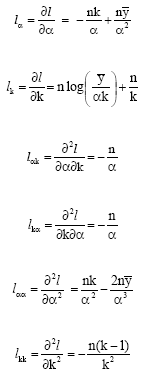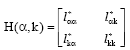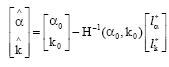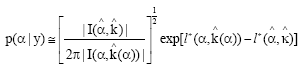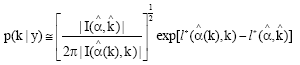Research Article
Bayesian Analysis of Gamma Distributions using S-PLUS and R Softwares
Department of Statistics, University of Kashmir, Srinagar, India
A. Ahmed
Department of Statistics, University of Kashmir, Srinagar, India
A.A. Khan
Division of Agricultural Statistics and Economics, SKUAST-Kashmir, Shalimar, Srinagar, India