Research Article
Propagation of Love Waves Through an Irregular Surface Layer in the Presence of an Infinite Rigid Strip
Maharshi Dayanand University, Rohtak, India
Pushpander Kadian
Maharaja Surajmal Institute, New Delhi, India
Love waves are transversally propagated surface waves which we feel directly during earthquake. The study of propagation of Love waves through crustal layer of earth gives us the idea about the internal structure of earth. In the present study we propose to discuss the effect of presence of an infinite rigid strip in the layer. A surface layer -H≤z≤0 is superimposed on a solid half space z≥0. The irregularity is in the form of an infinite rigid strip -H≤z≤-h, x≤0 in the surface layer and the other half of the layer is free surface.
This study finds its base on a paper by Sato (1961) who studied the problem of reflection and transmission of Love waves at a vertical discontinuity in a surface layer. Jardaneh (2004) has considered the expected source of earthquake evaluating the ground source response spectra taking into account local soil properties to evaluate seismic forces. Kaur et al. (2005) have studied the reflection and refraction of SH-waves at a corrugated interface between two laterally and vertically heterogeneous viscoelastic solid half-space. Dhaimat and Dhaisat (2006) have studied the sharp cut decrease of Dead Sea. The propagation of wave in inhomogeneous thin film has been discussed by Ugwu et al. (2007) using the series expansion solution method of Green’s function. Tomar and Kaur (2007) have studied the problem of reflection and transmission of a plane SH-wave at a corrugated interface between a dry sandy half space and an anisotropic elastic half space. They used the Rayleigh (1878) method of approximation for studying the effect of sandiness, the anisotropy, the frequency and the angle of incidence on the reflection and transmission coefficients. Ademeso (2009) has discussed the deformation traits in Charnockite rocks by analyzing the direction of maximum compressional and tensional stresses inferred from the rose diagram. Chattopadhyay et al. (2009) has studied the reflection of shear waves in viscoelastic medium at parabolic irregularity. The authors found that the amplitude of reflected wave decreases with increasing length of notch and increases with increasing depth of irregularity. The finite element method analysis has been used by Adedeji and Ige (2011) to investigate and compare the performance of a reinforce concrete bare frame infilled with or without straw bale wall shape memory alloy diagonal wires subjected to seismic loads and earthquake ground excitation. Ramli and Dawood (2011) have studied the effect of steel fibers on the engineering performance of concrete. A computational technique has been applied to study the field propagation through an inhomogeneous thin film using Lippmhhann-Schwinger equation by Ugwu (2011). The propagation of seismic waves has also been studied by Zaman (2001), Zhang and Chan (2003), Balideh et al. (2009), Saito (2010) and Aziz et al. (2011). Here, we discuss the propagation of Love waves through irregularity in form of an infinite rigid strip present in the surface layer.
THE PROBLEM AND ITS SOLUTION
The scattering of incident Love waves due to infinite rigid strip in the surface layer has been discussed in the present study. The problem is being analyzed in zx-plane. The z-axis has been taken vertically downwards and x-axis along the interface. The geometry of the problem is given in Fig. 1. The incident Love wave is given by:
| (1) |
| (2) |
Where,
| (3) |
and k1N is a root of equation:
| (4) |
μ1 and μ2 being the rigidities of shear waves in the half space and in the crustal layer, respectively.
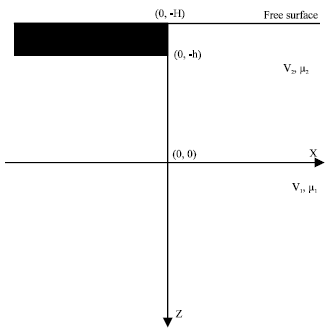 | |
| Fig. 1: | Geometry of the problem |
The wave Equation in two dimensions is given as:
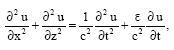 | (5) |
where, ε>0 is the damping constant and c is the velocity of propagation. If the displacement be harmonic in time, then:
| (6) |
and above equation reduces to:
| (7) |
The above wave equation in the present study can be written as:
| (8) |
Where,
| (9) |
V1 and V2 are, respectively the velocities of shear waves in the half space z≥0 and in the layer -H≤z≤0.
The total displacement is given by:
| (10) |
| (11) |
| (12) |
The boundary conditions are:
(i) | (13) |
(ii) | (14) |
(iii) | (15) |
(iv) | (16) |
(v) | (17) |
From Eq. 12, 13 and 15, we get:
| (18) |
| (19) |
Taking Fourier transform of Eq. 8, we obtain:
| (20) |
where, ![]() and
and ![]() represents Fourier transform of vj (x, z) which can be defined as:
represents Fourier transform of vj (x, z) which can be defined as:
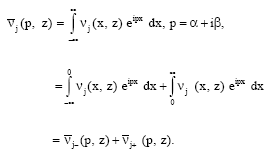 | (21) |
If for a given z, as |x|→∞ and M, τ> 0, |vj (x, z)|~Me-τ|x|, then ![]() is analytic in β>-τ and
is analytic in β>-τ and ![]() is analytic in β<τ (= lm (kj)). So by analytic continuation
is analytic in β<τ (= lm (kj)). So by analytic continuation ![]() and its derivatives are analytic in the strip -τ<β<τ in the complex p-plane. Solving Eq. 20 and choosing the sign of θj such that its real part is always positive, we obtain:
and its derivatives are analytic in the strip -τ<β<τ in the complex p-plane. Solving Eq. 20 and choosing the sign of θj such that its real part is always positive, we obtain:
| (22) |
| (23) |
Solving Eq. 22 and 23 by using boundary condition (Eq. 17), we get:
| (24) |
Differentiating Eq. 24 with respect to z, putting z = -h, denoting ![]() by
by ![]() etc. and then eliminating A (p), we obtain:
etc. and then eliminating A (p), we obtain:
| (25) |
Taking Fourier transformation of Eq. 16, we get:
| (26) |
Now, multiplying Eq. 8 by eipx and integrating from 0 to ∞ (j = 3), we find:
| (27) |
Changing p to -p in Eq. 27 and subtracting the resulting equation from Eq. 27, we get:
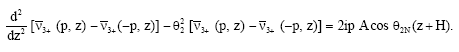 | (28) |
The solution of Eq. 28 is written as:
| (29) |
Using boundary condition (14) in Eq. 29, we find:
| (30) |
Differentiating Eq. 30 with respect to z, putting z = -h in resulting equation and in Eq. 30 and then eliminating D (p) from both equations, we get:
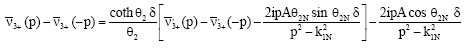 | (31) |
where, δ = H-h, is the width of the rigid strip. From Eq. 25 and 26, we write:
 | (32) |
Using Eq. 25 in Eq. 32, we get:
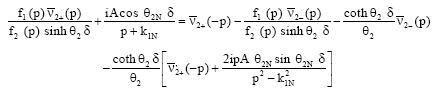 | (33) |
where,
| (34) |
| (35) |
Equation 33 is the Wiener-Hopf type differential equation (Noble, 1958) whose solution will give ![]() .
.
Solution of the Wiener-Hopf equation: For solution of Eq. 33, we factorize:
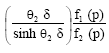 |
as given in Appendix 1, as:
| (36) |
where,
| (37) |
p = ±p1n and p = ±p2n are the zeros of f1 (p) and f2 (p), respectively.
We now decompose:
as:
| (38) |
where,
| (39) |
Now using Eq. 36 and 39 in Eq. 33, we find:
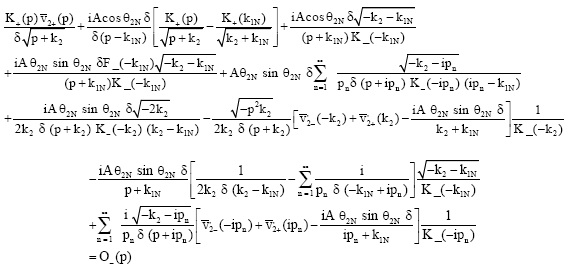 | (40) |
In Eq. 40, O_(p) include the terms which are analytic in β<τ and left hand member of above equation is analytic in the region β>-τ. Therefore, by analytic continuation each member tends to zero in its region of analyticity as |p|→∞. Hence by Liouville’s theorem, the entire function is identically zero. So equating to zero the left hand side of Eq. 40, we find:
 | (41) |
where,
| (42) |
| (43) |
| (44) |
The displacement v2 (x, z) is obtained by inversion of Fourier transform given as:
 | (45) |
where, ![]() is given in Eq. 41.
is given in Eq. 41.
RESULTS AND DISCUSSION
The incident Love waves are scattered when these waves encounter with surface irregularities like rigid strip in the crustal layer of earth. For finding the scattered component of the incident Love waves, we evaluate the integral in Eq. 45. There is a branch point p = -k2 in the lower half plane. The contour of integration has been shown in Fig. 2. For contribution around this point we put p = -k2-it, t being small. The branch cut is obtained by taking Re (θ2) = 0. Now θ22 = p2-k22 should be negative, so ![]() . The imaginary part of θ2 has different signs on two sides of the branch cut. Now integrating Eq. 45 along two sides of branch cut, we get:
. The imaginary part of θ2 has different signs on two sides of the branch cut. Now integrating Eq. 45 along two sides of branch cut, we get:
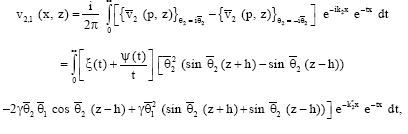 | (46) |
where, Ψ (t) and ξ (t) are given by:
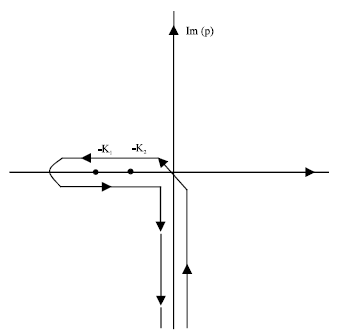 | |
| Fig. 2: | Contour of integration in complex p-plane |
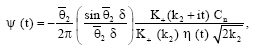 | (47) |
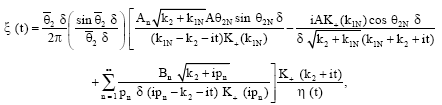 | (48) |
and
| (49) |
For evaluation of integral in Eq. 46, Laplace transforms (Oberhettinger and Badii, 1973) as given in Appendix 2 are used. Since ‘t’ is small, so we retain ξ (0) and Ψ (0) only. Also for:
and Eq. 46 is written as:
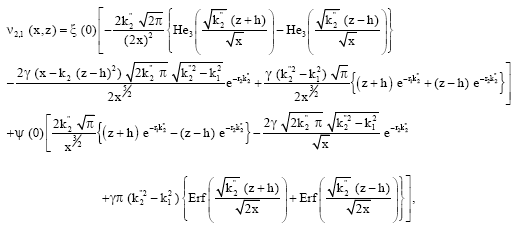 | (50) |
where, Erf (x) is the error integral and He3 (x) is the Hermite polynomial of order 3, given as:
| (51) |
and
| (52) |
| (53) |
For large x, we can write:
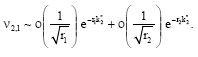 | (54) |
Equation 54 represent the scattered waves at large distance having the amplitude of cylindrical waves originating at the point (0,-h), the tip of the strip and at the point (0, h), the image of tip in the interface.
The incident Love waves are not only scattered but they are reflected also by the surface irregularity. For finding the reflected component, we evaluate the integral in Eq. 45 in lower half plane when x>0. There is a pole at p = -k1N and the corresponding wave is given as:
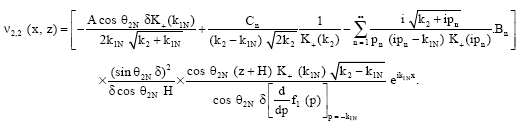 | (55) |
These are the reflected Love waves in the region -h≤z≤0, x>0. Now, we find the reflected component of the waves in the region -H≤z≤-h, x≥0. The displacement in this region is given as:
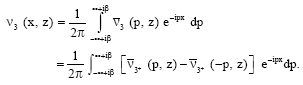 | (56) |
Putting z = -h in Eq. 30, we write:
| (57) |
Eliminating D (p) from Eq. 30 and 55, we find:
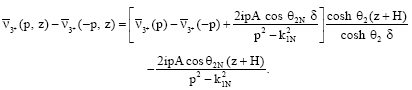 | (58) |
Now using Eq. 26 (54) and 56, we obtain:
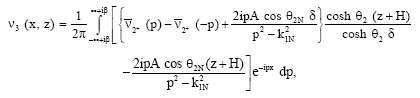 | (59) |
where, ![]() is given by Eq. 41 and
is given by Eq. 41 and ![]() is obtained by replacing p by -p in Eq. 41. There is a simple pole at p = -k1N and the residue at this point contributes to the reflected wave in the region -H≤z≤-h, x≥0 which is given by:
is obtained by replacing p by -p in Eq. 41. There is a simple pole at p = -k1N and the residue at this point contributes to the reflected wave in the region -H≤z≤-h, x≥0 which is given by:
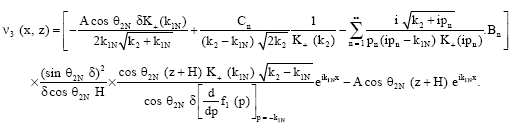 | (60) |
Equation 60 represents the wave reflected in the region -H≤z≤-h, x≥0, in presence of the rigid strip. The first term in the equation is same as in Eq. 55 and this represents the wave reflected from the free surface (z = -H, x≥0) of the layer and the second term represents the wave reflected by the rigid strip (-H≤z≤-h, x = 0). We now evaluate the integral in Eq. 45 in upper half plane if x<0. There is a pole at p = k1N which contributes to:
| (61) |
which cancels the incident wave when x<0. Now, for finding the transmitted Love waves of mth mode, let p = k2m be the roots of the Equation:
| (62) |
The residue at the poles p = k2m contributes to:
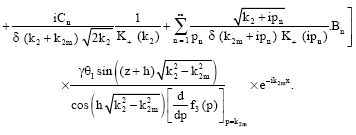 | (63) |
These are the transmitted Love waves of mth mode in the surface layer of thickness h which are absent on the line z = -h.
The scattered waves decrease as the distance increases and they behave as decaying cylindrical waves at the distant points. So, as the distance from the strip increases, the component of the scattered wave decreases which specifies that at large distance from the strip, the destructive effect of these waves is comparatively low. If whole of the surface layer is rigid, the scattered waves behave as cylindrical waves and the transmitted waves propagate with a velocity equal to that of the shear waves in the solid layer. The transmitted waves decrease exponentially as the distance from the strip increases. It is also clear that as the width of strip decreases, the transmitted component of the waves give larger value.
APPENDIX
Appendix 1: Decomposition of:
According to infinite product theorem, we can write:
| (A1) |
Where:
| (A2) |
Now if p = ±p1n and p = ±p2n are zeros of f1 (p) and f2 (p), respectively, we can write:
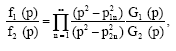 | (A3) |
Where:
 |
and
| (A4) |
and G1 (p) and G2 (p) have no zeros. Also we can write:
| (A5) |
Where:
| (A6) |
and
| (A7) |
| (A8) |
tan φ2 and tan ![]() are obtained from (A7) and (A8) by replacing H by h.
are obtained from (A7) and (A8) by replacing H by h.
Now, from (A1), (A3) and (A5), we write:
| (A9) |
and
| (A10) |
and |k+(p)|→|p|1/2, as |p|→∞.
Appendix 2: Laplace transforms used are:
| (B1) |
| (B2) |
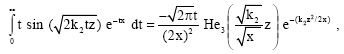 | (B3) |
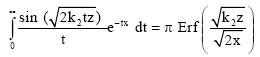 | (B4) |
 | (B5) |