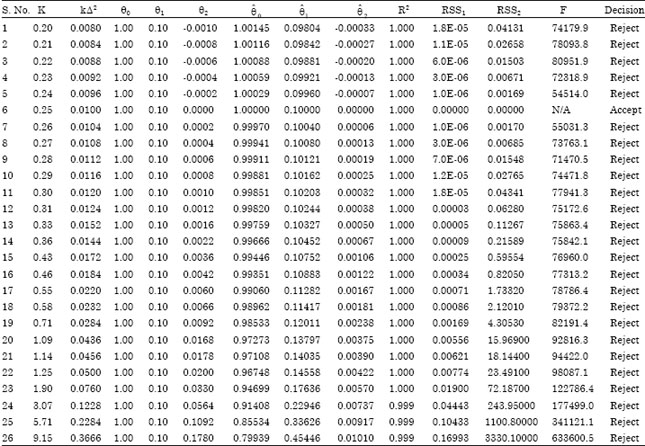
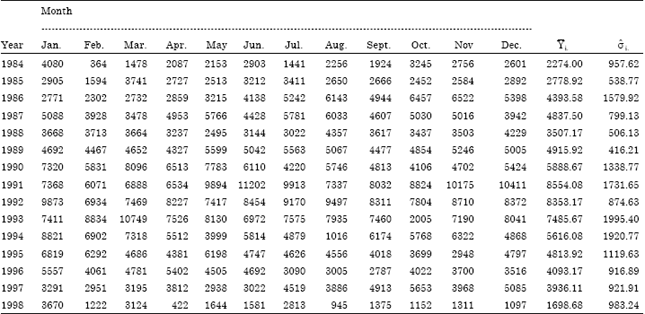
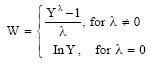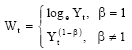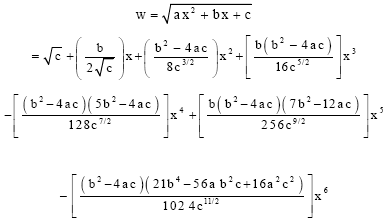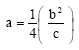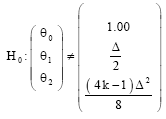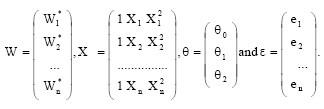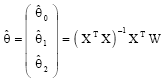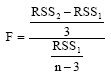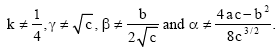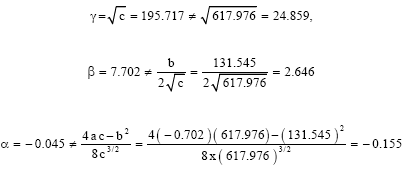Research Article
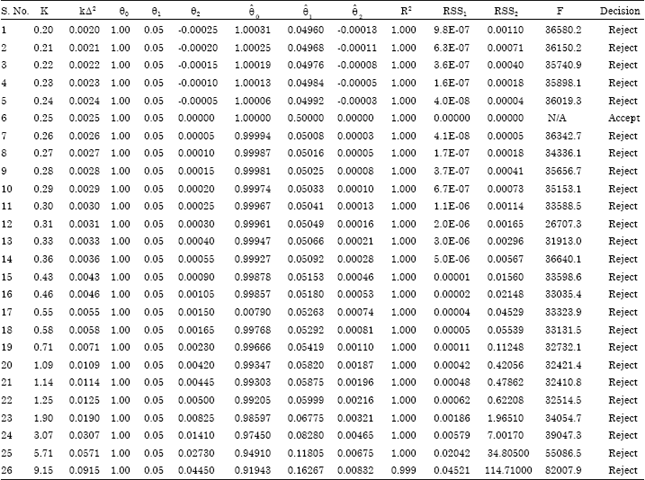
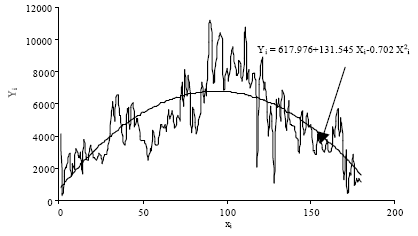
Square Root Transformation of the Quadratic Equation
Department of Statistics, School of Science, Federal University of Technology, P.M.B. 1526, Owerri, Imo State, Nigeria
Johnson Ohakwe
Department of Mathematics and Statistics, Faculty of Science, Anambra State University, P.M.B. 02, Uli, Anambra State, Nigeria