Research Article
Maximal Queue Size with Standard Normal Distribution for Arrival Times
Department of Mathematics, Faculty of Science, Port Said University, Port-Said, Egypt
LiveDNA: 20.4959
ORCID: 0000-0002-4657-3045
INTRODUCTION AND DESCRIPTION OF THE PROBLEM WITH ITS SOLVING
Luczak and McDiarmid (2006) has done study in the supermarket model and considered that the distribution of the arrival of customers follows the Poisson distribution, the model Mx/G/1 was in working by Koole et al. (2005) has also Poisson distribution for arrival of customers but in the study of Sadowsky and Szpankowski (1992) was in Multi-server G/G/c queue where the distribution of arrival customers is general distribution. Tadj and Hamdi (2001) performed maximum entropy solution to a quorum queueing system. The M/G/1 FB Queue was performed by Nuyens (2004) and carried out the Maximum Queue Length for Heavy-Tailed Service Times. Artalejo et al. (2007) carried out algorithmic analysis of the maximum queue length in a busy period for the M/M/c retrial queue. In this study added a new case involving distribution of inter-arrival times of customers follows the standard normal distribution. The aim to get the formula of the probability of the maximum queue length in the system at this new case.
Let qn be the number of customers found in the system immediately prior to the arrival of the n th customer Cn. The sequence {qn} forms a discrete state Markov chain. Also, let Xn+1 be the number of customers served between Cn and Cn+1. Thus qn+1 = qn+1-Xn+1, where Xn+1≤qn. Since the service distribution is exponential with rate μ, It follows that:
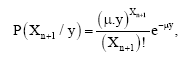 |
where, y is the time between consecutive arrivals, Let:
where, γk (y) is the number of customers in the queue at time y, under the condition that at the time 0 the customer enters the system which already contains k customers. Thus at the time 0 there are k customers in the queue and one is being serviced. It is evident that:
where: A1 is the event that a customer arrived at time y, ![]() and k = 0, 1, ..., n given that y varies from zero to t. A2 is the event that a customer arrived at time y,
and k = 0, 1, ..., n given that y varies from zero to t. A2 is the event that a customer arrived at time y, ![]() and given that y varies from zero to t. A3 is the event that no customer arrived during the time interval [0,t] ≡ the event that the inter-arrival time is greater than t. It is clear that:
and given that y varies from zero to t. A3 is the event that no customer arrived during the time interval [0,t] ≡ the event that the inter-arrival time is greater than t. It is clear that:
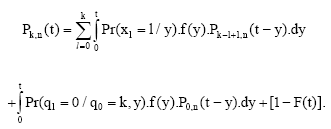 |
But:
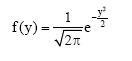 |
And:
 |
Let: y = r sin θ, z = r cos θ,
Then: dy.dz = rdr.dθ, where,
and ![]() it follows that:
it follows that:
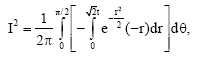 |
 |
Hence:
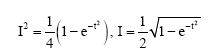 |
Therefore,
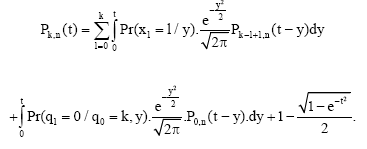 |
But:
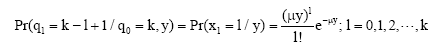 |
And:
 |
Hence:
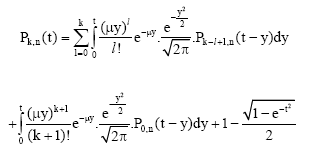 |
Therefore:
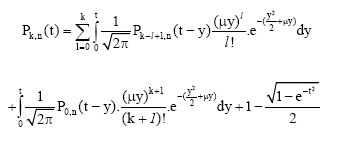 |
where, ![]()
Similarly:
 |
And:
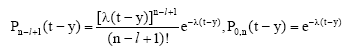 |
Then:
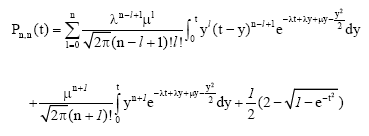 | (1) |
Application: Suppose that: Arrival rate = λ = 1, Service rate = μ = 2, t = time in min = 1, 2, 3 n = maximum queue length = 12, 13, 14, 15, 16.
Applying the last formula for the probability of a maximum length of a queue in the system during the period of time t and using mathematic program on the Eq. 1 as follows:
If t = 1, then:
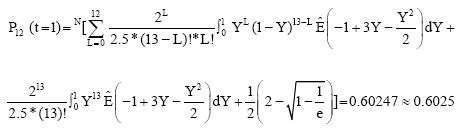 |
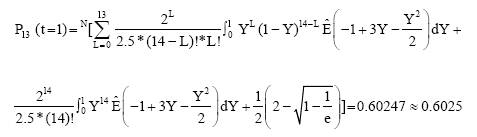 |
Similarly, P14 (t = 1) = P15 (t = 1) = P16 (t = 1) = 0.60247≈0.6025.
On the other hand, when t = 2, then we can get:
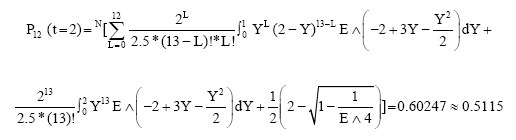 |
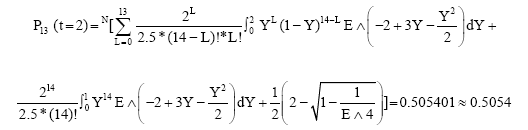 |
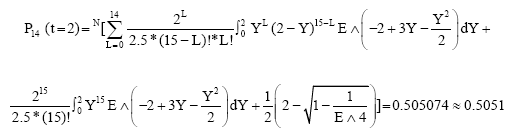 |
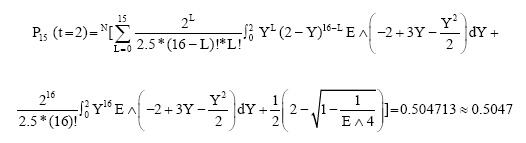 |
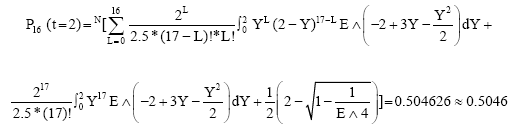 |
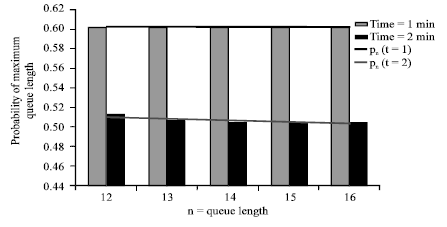 | |
| Fig. 1: | Maximum queue lengths and its probabilities |
From Fig. 1 we can deduce the following information:
| • | Probabilities for a maximum length of a queue are approximately equality and equal to a fixed amount at t = 1 min. means that as long as the time a small odds are the maximum length of a queue is approximately equal and equal to a fixed amount and the relationship between these probabilities and the maximum length of the queue to be a linear relation as the following: |
| • | Similarly, in the case of t = 2 min. the linear relation is written as follows: |
But, when t≥3 the values of the probabilities of the maximum queue length will be greater than one, so this is contradictory that because:
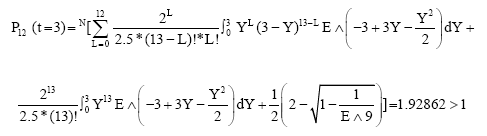 |
Similarly, The values of P13 (t = 3), P14 (t = 3), P15 (t = 3), P16 (t = 3) will greater than 1. Thus, we can estimate the limits of time appropriate to the values of the maximum lengths of queues in the system or try to change the service rate or the rate of arrival or the values of the maximum length of a queue as long as we have been given that and reiterate once again enter the values in the formula that we have to get the desired results.