ABSTRACT
In this study, we studied the zeta function with a 2-dimensional shift of finite type via left and upward shifts, on a subspace of the space of doubly indexed sequences over a finite abelian compact group and new way to calculate periodic point numbers based on the study of linear algebra of F2 the field and index subgroup. We showed the periodic point data of 2-dimensional shift of finite type via left and upward shifts.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/ajms.2011.151.160
URL: https://scialert.net/abstract/?doi=ajms.2011.151.160
INTRODUCTION
Let G be a finite abelian group. We consider our study here when G = {0,1}, XG = GZ2 be the space of doubly indexed sequences over G and it is subspace
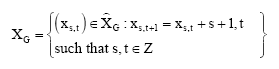 |
The two-dimensional shift of finite type α: XG → XG defined by:
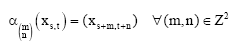 |
of the space GZ2 of doubly indexed sequences over a finite abelian compact group G. The space XG was introduced by Ward (1993).
To fined the Zeta function, it requires from us study the periodic points in XG by α: XG → XG.
The group Z2 acts natural on the space XG via left and upward shifts we show the periodic point data of XG determine the group G.
This allows us to view XG as a Z2-space for every subgroup U of Z2, we define U-periodic point to be those x ε XG by the action of the subgroup U. This is natural generalization of the notion of periodic points in case of any ordinary Z-action. If U has finite index in Z2, the number FU of U-periodic points x ε XG is finite.
Compare this situation to the full shift, i.e., the shift action on the space XG. If the index of U in Z2 is m, then obviously FU = |G|m for any group G.
It was also introduced by Lind (1996), Roettger (2005) and Al-Refaei and Noorani (2007) new way to calculate periodic point numbers based on the study of linear algebra of F2 the field and get the zeta function which generality by Lind (1996).
Huffman code has been widely used in text, image and video compression. For example, it is used to compress the result of quantization stage in JPEG (Hashemain, 1995). The simplest data structure used in the Huffman decoding is the Huffman tree. Array data structure (Chen et al., 1999) has been used to implement the corresponding complete ternary tree for the Huffman tree.
Modeling and simulation of thermal dynamic system has been studied by Bhatti et al. (2006). Whereas, Shabbak et al. (2011) proposed multivariate control chart which is less sensitive to the sustained shift in mean process. Another related work has been proposed by Abu-Shawiesh et al. (2009) and Goegebeur et al. (2005).
Huffman code has been widely used in text, image and video compression. For example, it is used to compress the result of quantization stage in JPEG (Hashemain, 1995). The simplest data structure used in the Huffman decoding is the Huffman tree. Array data structure (Chen et al., 1999) has been used to implement the corresponding complete ternary tree for the Huffman tree.
Here our study will be about the compact group G = {0,1}. And so we observe that there are several of subgroups U of Z2 with finite indexes but in our work here we can classify the periodic points for subgroups U of Z2.
CALCULATION FOR THE ZETA FUNCTION
Here, we will introduce the formula for the zeta function of left and upward shifts α according to the quality of the subgroups which are used in the following propositions:
Proposition 1: The zeta function of a 2-dimensional shift of finite type via left and upward shifts α according to his subgroups U of Z2 in the formula (2) which defined as follows:
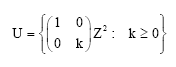 | (2) |
Will be given by ζx (Z) = 1/1-Z
Proof: It was introduced by Ward (1993) and Lind (1996) that for finite abilean (xs, I) ε XG is a U-periodic point if and only if:
| (3) |
The number of periodic points for the special subgroups U as in (2) is exactly the No. of solutions to Eq. 3.
In this case at G = {0,1} we observe that for (xs, I) ε XG, xs,i will be 0 or 1. And for appositive integer k = 0, 1, 2. We observe that 2k-1 is odd No. Then (2k-1) 0 = 0 and (2k-1). That is, for any subgroup U of Z2 in the formula (2), the zero-element will be only periodic point, i.e., FU = 1.
Hence the zeta function will define by:
 |
ζx (Z) = exp (-log (1-Z)) = 1/1-Z
Proposition 2: The zeta functions of a 2-dimensional shift of finite type via left and upward shifts α according to the subgroups U of Z2 which defined as follows:
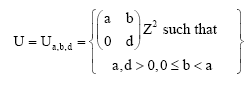 | (4) |
Will be given by:
Proof: It was introduced by Ward (1998) that (xs, I) ε XG is an U-periodic point if and:
| (5) |
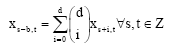 | (6) |
The No. of periodic points for the special subgroups U as in (4) is exactly the No. of solutions to Eq. 5, 6 above.
When G = {0, 1}, we observe that for (xs, I) ε XG will be 0 or 1. Hence, for appositive integer m = 0, 1, 2… we observe
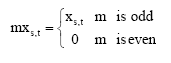 |
From definition of XG , for (xs, I) ε XG must satisfy the following equation :
| (7) |
We observe that the equation has four solutions:
 |
Hence, if the System for Eq. 5, 6 has an unique solution, then for any subgroup U of Z2 in the formula (4), the zero-element will be only periodic point, i.e., FU = 1. And if the system for Eq. 5, 6 has more than one solution, then by the solutions for Eq. 7, for any subgroup U of Z2 in the formula (4), FU = 4.
Now we will take some special cases in this formula as follow:
| • | If a = 1, c = 1, b = 0 then from Eq. 5, 6 we get: |
| xs, i+1 = xs, I + xs+1, I |
| xs,i = xs+1, t and xs, I = xs, I +xs+1, t this implies to |
xs,i = 0, hence Fu = 1.
| • | If a = 2, b = 1, d = 1 then from Eq. 5 and 6, we get |
| (8) |
| (9) |
From Eq. 8 xs-1, t and from 9 xs, I this implies to FU = 1
| • | If a = 3, b = 4, d = 1 then from Eq. 5 and 6, we get |
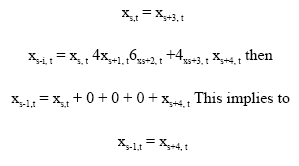 |
Then this equation has more then one solution therefore FU = 4
We can continuous by the same way to calculate the periodic points for some special cases again as showed in Table 1.
Where, a, d>0, 0≤b <a and FU is the periodic point.
Hence, we can define the zeta function by:
| Table 1: | Periodic points for some special cases |
 | |
Proposition 3: The zeta function of a 2-dimensional shift of finite type via left and upward shifts α according to the subgroups U of Z2 which defined as follows:
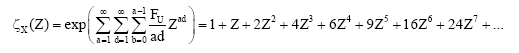 |
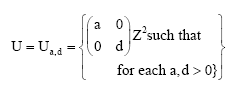 | (10) |
will be given by:
Proof: We observe that the formula (10) is special case from the formula (4) by make b = 0. Hence, we can put b = 0 in the Eq. 6 to get that:
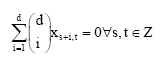 | (11) |
Now we will take some special cases in this formula as follow:
| • | We observe that if a = 1 and d is even No. then from Eq. 5 and 6 we get: |
xs, t = xs+a, t And |
| (12) |
This is implies to:
We observe that ![]() is even number for 1≤ I < d Hence, from (12) we get:
is even number for 1≤ I < d Hence, from (12) we get:
 |
| • | If a = 1 and d = 1 then from Eq. 5 and 6 we get: |
| (13) |
| (14) |
From Eq. 13 we observe that:
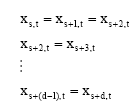 |
Hence from Eq. 14 we get:
| • | If a = 2 and d = 1 then from Eq. 5 and 6 we get: |
| (15) |
| (16) |
If d is even then from (1) we get that FU = 1
If d is odd then from (15) we observe that:
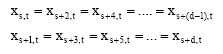 |
Hence, from Eq. 16 we get that xs+(d-1), t, this implies to FU = 1.
Then e we can define the zeta function by:
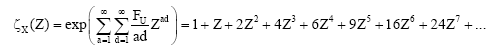 |
We can also compute FU using some linear algebra over G (we can consider G a field). A point x ε XG that is U-invariant must have horizontal periodic a, so is determined by an:
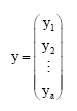 |
element from the vector space Fa2.
Let Ia be axa identity matrix. Let Pa be axa permutation matrix corresponding to the cyclic shift of elementary basis vectors Fa2.
The condition of U-periodicity of (xs,t) translates to the condition:
| (17) |
Hence:
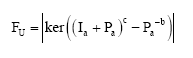 |
Then the zeta function in this case equal:
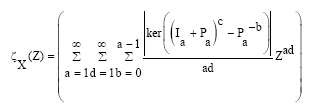 |
We will take some cases in this form
| • | If a = 1, c = 1, b = 0, then, |
Pa + Ia = 2 Then y = y ⇒ y = 0 because
2*1 = 0 ≠ 1 not allow so 2*0 = 0. Hence FU = 1
| • | If a = 1, d = r, b = 0, then |
2r y = y ⇒ y = 0. Then FU = 1.
| • | If a = 2, d = 1, b = 0 Then: |
 |
Hence:
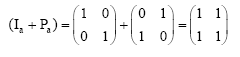 |
Let 
Hence:
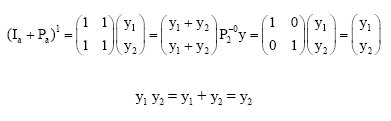 |
There fore y1 = y2,
Either y1 = 0, y2 ⇒ y1 y2 = 0 is possible or y1 = 1 is impossible because y2 ⇒ y1 y2 = 0 but y1 y2 = y1 is not zero. Hence FU = 1.
| • | If a = 2, d = 1, b = 0. Then: |
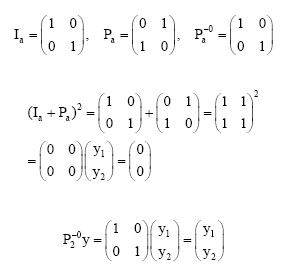 |
Then y1 = y2 = 0. Hence FU = 1.
Let a = 2 , d = 2, b = 0:
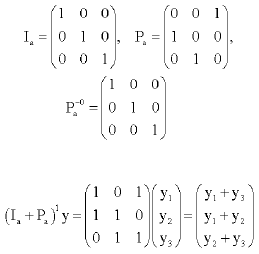 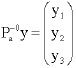 |
The we get that y1 = 0, y2 = 0 . Hence FU = 1.
And when a = 2, d = r, b = 0, then FU = 1. When a = 3, d = 1, b = 0 we get that:
Then:
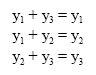 |
So y1 = y2 = y3 = 0, therefore, FU = 1.
Also similarly, when a = 3, d = 1, b = 1, we get that:
 |
 |
 |
Let y1 = 0 ⇒ y3 = y2 then y3 = 1 and y3 = 0, y2 = 0 and let:
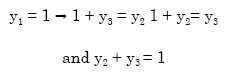 |
So:
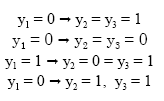 |
Hence, FU = 4.
Also when a = 3, d = 1, b = 2, similarly, FU = 1.
In the same way, we can get in all theses cases (a = 3, d = 2, b = 0), (a = 3, d = 2, b = 1) that FU = 1 and in these cases (a = 3, d = 2, b = 2), (a = 3, d = 3, b = 0) that FU = 1..
By using Mathematica, we will get this result:
CONCLUSIONS
The periodic point was calculated by using two methods namely, the index subgroup and the linear algebra of the field F2. According to these two methods, the Zeta function for two dimensional shift of finite type by left and upward shifts α has been studied. For validation of the present results, three cases study have been presented to get the Zeta function.
REFERENCES
- Abu-Shawiesh, M.O., F.M. Al-Athari and H.F. Kittani, 2009. Confidence interval for the mean of a contaminated normal distribution. J. Applied Sci., 9: 2835-2840.
CrossRefDirect Link - Bhatti, M.A., L.C. Xi and Y. Lin, 2006. Modeling and simulation of dynamic systems. J. Applied Sci., 6: 950-954.
CrossRefDirect Link - Chen, H., Y. Wag and Y. Lan, 1999. A memory-efficient and fast Huffman decoding algorithm. Inform. Process. Lett., 69: 119-122.
CrossRefDirect Link - Goegebeur, Y., V. Planchon, J. Beirlant and R. Oger, 2005. Quality assessment of pedochemical data using extreme value methodology. J. Applied Sci., 5: 1092-1102.
CrossRefDirect Link - Hashemain, R., 1995. Memory efficient and high-speed search huffman coding. IEEE Trans. Commun., 43: 2576-2581.
CrossRefDirect Link - Roettger, C.G.J., 2005. Periodic point classify a family of Markov shifts. J. Number Theory, 113: 69-83.
CrossRef - Shabbak, A., H. Midi and M.N. Hassan, 2011. The performance of robust multivariate statistical control charts based on different cutoff-points with sustained shift in mean. J. Applied Sci., 11: 56-65.
CrossRefDirect Link - Ward, T.B., 1993. An algebraic obstruction to isomorphism of Markov shifts with group alphabets. Bull. London Math. Soc., 25: 240-246.
CrossRef - Ward, T., 1998. A family of Mrkov subshift (almost) classified by periodic point. J. Number Theory, 71: 1-11.
CrossRef








