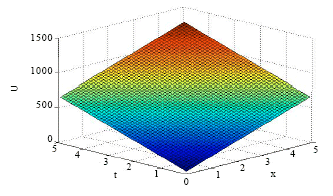
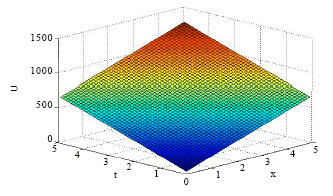
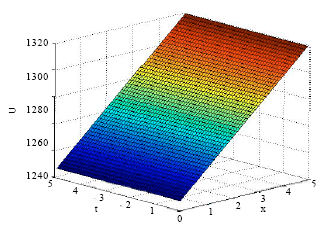
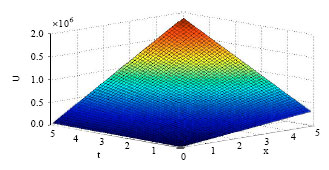
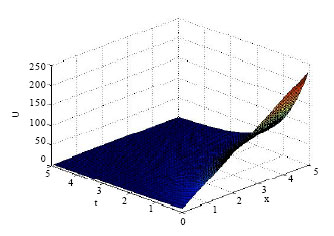
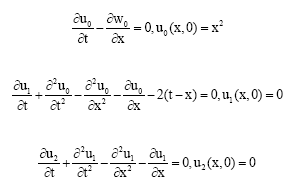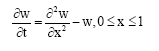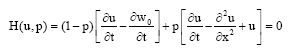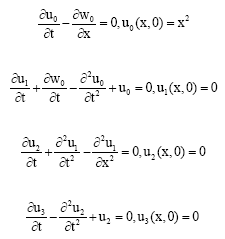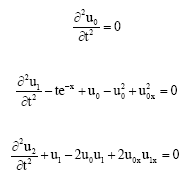Research Article
Applications of Homotopy Perturbation Method to Partial Differential Equations
Department of Mathematics, University of Rajasthan, Jaipur-302055, India
Giriraj Methi
Department of Mathematics, Poornima College of Engineering, Jaipur-302055, India