ABSTRACT
A two-dimensional sofic system has been defined by using the notion of allowable block. This definition is an extension of the original definition in the one-dimensional case. It is shown that the present definition is equivalent to using the notion of symbolic factors of subshift of finite types and to point out some of the phenomena which arise in the transition from classical shift of finite type
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/ajms.2011.109.112
URL: https://scialert.net/abstract/?doi=ajms.2011.109.112
INTRODUCTION
We shall give some definitions that are natural extensions to the two-dimensional case of similar notions that are well-known in the one-dimensional case (Lind and Marcus, 1995; Kitchens, 1998). We begin with the dynamical system and its subsystems which are of interest to us.
Modeling and simulation of thermal dynamic system has been studied by Bhatti et al. (2006). Whereas Shabbak et al. (2011) proposed multivariate control chart which is less sensitive to the sustained shift in mean process. Another related work has been proposed by Abu-Shawiesh et al. (2009) and Goegebeur et al. (2005).
Huffman code has been widely used in text, image and video compression. For example, it is used to compress the result of quantization stage in JPEG (Hashemain, 1995). The simplest data structure used in the Huffman decoding is the Huffman tree. Array data structure (Chen et al., 1999) has been used to implement the corresponding complete ternary tree for the Huffman tree.
Let A be a finite set and the set ![]() be the set of all maps x: Z2→A. For every we denoted by
be the set of all maps x: Z2→A. For every we denoted by ![]() the projection
the projection ![]() ,
, ![]() , where, x|E is the restriction of x: Z2→A to E if
, where, x|E is the restriction of x: Z2→A to E if ![]() and n
and n![]() Z2 then xn is the n-th coordinate of x, i.e., the value of x at n. We define, for every m
Z2 then xn is the n-th coordinate of x, i.e., the value of x at n. We define, for every m![]() Z2, a homomorphism σm of
Z2, a homomorphism σm of ![]() by setting (σmx)n = xm+n.
by setting (σmx)n = xm+n.
A closed subset ![]() is shift invariant (or a subshift of
is shift invariant (or a subshift of ![]() ) if σm (X) = X,
) if σm (X) = X,![]() m
m![]() Z2. If there exist a finite set F⊂Z2 and a set P⊂AF such that
Z2. If there exist a finite set F⊂Z2 and a set P⊂AF such that ![]() . The set P⊂AF is the collection of permissible (or allowed) words of X.
. The set P⊂AF is the collection of permissible (or allowed) words of X.
Example 1: Let, F = {(0,0), (1,0), (0,1)}⊂Z2 and P = {(t(0,0)), (t(1,0)), (t(0,1))![]() TF: t(0,0)+t(1,0)+t((0,1)) = 0}. Here the alphabet set A = {0, 1} and addition is W.r.t modulo 2 arithmetic. Then:
TF: t(0,0)+t(1,0)+t((0,1)) = 0}. Here the alphabet set A = {0, 1} and addition is W.r.t modulo 2 arithmetic. Then:
| (1) |
Given 2 directed graph GH and GV with the same set of edges ε we now define the edge shift:
 | (2) |
Definition 2: Let X = X(GH, GV) be an edge shift. Also let λ:ε→A be a map where A is some finite set, a sofic shift S with presentation (GH, GV, λ) is defined by S = {λ∞ (ξ): ξ∈X (GH, GV)} and λ∞ (ξ)(i, j) = λ(ξ(i, j)).
Definition 3: Let X1, X2 is topological space and Z2 acts on X1, X2 by a commuting homomorphism. For each n∈Z2, the action is written as n.x where x∈X1 to represent ![]() . Whenever n = (n1, n2). Similarly for x
. Whenever n = (n1, n2). Similarly for x![]() X2,
X2, ![]() , we say X2 is a factor of X1 if there exist a continuous onto map φ: X1→X2 such that φ (n.x) = n.φ (x).
, we say X2 is a factor of X1 if there exist a continuous onto map φ: X1→X2 such that φ (n.x) = n.φ (x).
When dealing with shift spaces, Curtis- Hedlund-Lyudon,s theorem says that the factor map is a sliding block code, i.e., there exist positive integers m, n, r. S and Φ: B(n+m+1)x(s+r+1) (X1)→ A (X2):
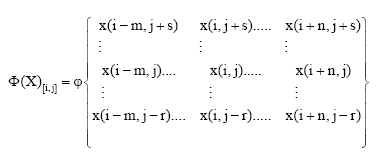 | (3) |
Here B(n+m+1)x(S+r+1) (X1) denotes the rectangular allowable blocks of size (n+m+1)x(s+r+1) and A (X2) is the alphabet set of X2. From the above work and by Al-Refaei et al. (2007) we get this result.
Proposition 4: Every edge shift is a shift of finite type.
Proof: Given X = X(GH, GV), fined F and P such that X = X(F, P) X has alphabet ε = ε (GH) = ε (GV).
Take ![]()
Take:
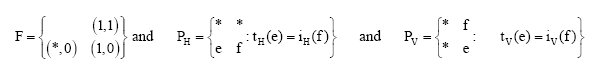 |
Then P = PH∪PV. In fact, it is a matrix subshift with transition matrix H and V defined as follows:
H and V is of size |ε|H*ε| record ε so that each are {e1, e2, e3,ÿ, w|ε|}.
The define:
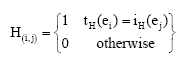 |
Similarly for V.
Definition 5: Let X = X (GH, GV) be an edge shift. Also let λ:ε→A be a map where A is some finite set. A sofic shift S with presentation (GH, GV, λ) is defined by S = {λ∞ (ξ): ξ∈X (GH, GV)} and:
| (4) |
Proposition 6: If S a sofic system then S is a factor of shift of finite type.
Proof: Let (GH, GGVλ) be presentation of S .By definition there exist edge shift X = X(GH, GV) and a map λ∞: X→S which is onto. Also λ∞ commutes with the respective shift maps on X and S. Thus S is a factor of X via λ![]() .
.
The result follows since X is a shift of finite type.
Proposition 7: Let X be shift of finite type and Y is shift space φ: X→Y be factor map. Then Y is a sofic system.
Proof: First by going to higher block system one can find an edge shift X' which is isomorphic to X. Let Φ be the associated map that induced Φ: X→Y. If we denote by ε the set of edges arising from the graphs of the edge shift X', then one can define a map λ: ε→A (Y) by λ' (e) = Φ (e), ∀e∈ε. It is then an easy matter to check for commutatively so that λ and the respective graphs is the presentation of the sofic system.
Theorem 8: A two-dimensional shift space ![]() is two-dimensional sofic system if and only if a factor of two-dimensional shift of finite type.
is two-dimensional sofic system if and only if a factor of two-dimensional shift of finite type.
Proof: Let is sofic shift and ![]() be presentation of X The 1x1-block map λ induces a sliding block code λ:χ(GH, GV)→χS that is onto by definition of.
be presentation of X The 1x1-block map λ induces a sliding block code λ:χ(GH, GV)→χS that is onto by definition of.
Hence X = χS is factor of edge shift χGH and χGV which has finite type. Conversely, suppose that ![]() a shift space for which there is two-dimensional shift of finite type Y and a factor map φ: Y→X let φ have memory m(r) and anticipation m (s) then φ is induced by Φ on Bm(r)+n(s)+1(Y) by increasing m(r) if necessary .We can assume that Y is [m(r)+n(s)]-step. Define Ψ: Y→Y[m(r)+n(s)+1] by Ψ(y)[i, j] = y [I-m, j+s and I+n, j+s].
a shift space for which there is two-dimensional shift of finite type Y and a factor map φ: Y→X let φ have memory m(r) and anticipation m (s) then φ is induced by Φ on Bm(r)+n(s)+1(Y) by increasing m(r) if necessary .We can assume that Y is [m(r)+n(s)]-step. Define Ψ: Y→Y[m(r)+n(s)+1] by Ψ(y)[i, j] = y [I-m, j+s and I+n, j+s].
Ψ Almost the same the higher block map Bm(r)+n(s)+1 except that. We use coordinates from y starting at index I-m, j+s rather than i, j. Since y is (m(r)+n(s))-step so, there is graphs GH, GV with edges named by block Bm(r)+n(s)+1 (Y) So That Y[m(r)+n(s)+1] = X(GHGV). Define a labeling λ on GH, GV by λ (e) = Φ (e). We will show that S = (χ(GH, GV), λ) is presentation of X proving that X is Sofic observe that Fig. 1 is commutes for if yεY, then φ (y)[i, j] = Φ (y[i-m, j+s and I+n, j+s]).
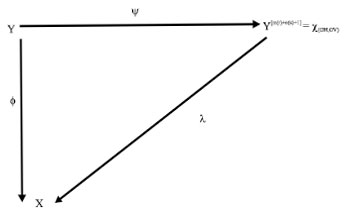 | |
| Fig. 1: | Two dimensional shift |
While λ (Ψ (y)[i, j]) = λ (Ψ (y)[i, j]) since Ψ is conjugacy, the image of φ and of, λ are equal hence X = φ (y) = = λ(χGHV,GV) so that S is presentation of X.
REFERENCES
- Abu-Shawiesh, M.O., F.M. Al-Athari and H.F. Kittani, 2009. Confidence interval for the mean of a contaminated normal distribution. J. Applied Sci., 9: 2835-2840.
CrossRefDirect Link - Bhatti, M.A., L.C. Xi and Y. Lin, 2006. Modeling and simulation of dynamic systems. J. Applied Sci., 6: 950-954.
CrossRefDirect Link - Chen, H., Y. Wag and Y. Lan, 1999. A memory-efficient and fast Huffman decoding algorithm. Inform. Process. Lett., 69: 119-122.
CrossRefDirect Link - Goegebeur, Y., V. Planchon, J. Beirlant and R. Oger, 2005. Quality assessment of pedochemical data using extreme value methodology. J. Applied Sci., 5: 1092-1102.
CrossRefDirect Link - Hashemain, R., 1995. Memory efficient and high-speed search huffman coding. IEEE Trans. Commun., 43: 2576-2581.
CrossRefDirect Link - Shabbak, A., H. Midi and M.N. Hassan, 2011. The performance of robust multivariate statistical control charts based on different cutoff-points with sustained shift in mean. J. Applied Sci., 11: 56-65.
CrossRefDirect Link








