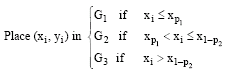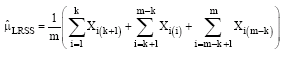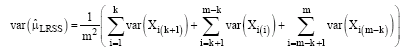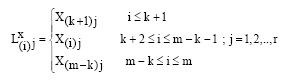Research Article
Efficient Wald Type Estimators for Simple Linear Measurement Error Model
Dipartimento di Scienze Pedagogiche, Psicologiche e Didattiche, Decorate Course in Sciences of the Mind and Human Relations, Universit� del Salento, Lecce, Italia
A. Al-Nasser
Department of Statistics, Science Faculty, Yarmouk University, Irbid, Jordan
E. Ciavolino
Dipartimento di Filosofia e Scienze Sciali, Universit� del Salento, Lecce, Italia