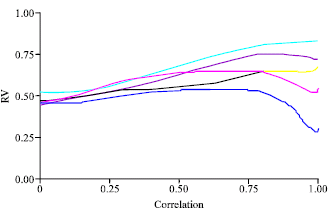
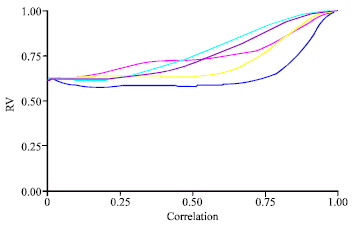
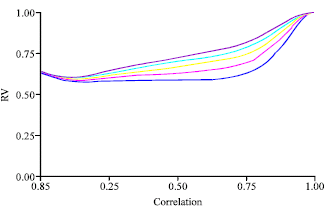
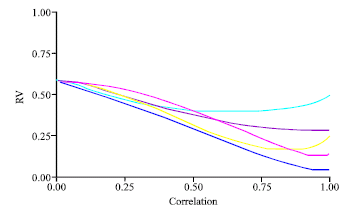
Research Article
Some Data Reduction Methods to Analyze the Dependence with Highly Collinear Variables: A Simulation Study
Department of Strategy and Quantitative Methods, Second University of Naples, Via Gran Priorato di Malta, 81043 Capua (Caserta), Italy
P. Sarnacchiaro
Department of Mathematics and Statistics, University Federico II, Naples, Traversa Michele Pietravalle, 4-CAP 80131, Italy