Research Article
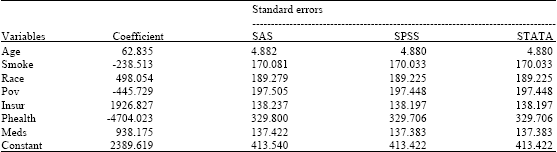
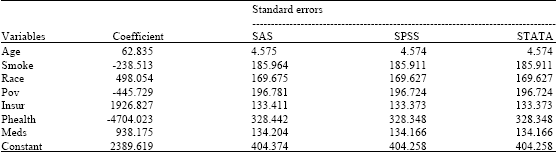
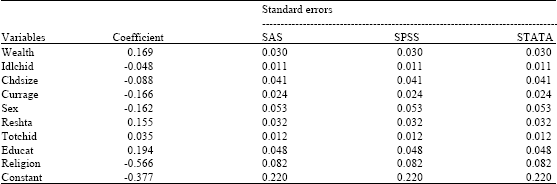
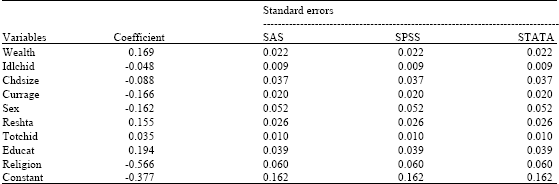
Complex Survey Data Analysis: A Comparison of SAS, SPSS and STATA
Department of Statistics, University of Ilorin, P.M.B. 1515 Ilorin, Nigeria
LiveDNA: 234.3615
A.A. Adewara
Department of Statistics, University of Ilorin, P.M.B. 1515 Ilorin, Nigeria
LiveDNA: 234.4853
R.A. Adeyemi
Department of Crop Production, Federal University of Technology Minna, Minna, Nigeria