ABSTRACT
The Bugeaud-Mignotte theorem concerns the Diophantine equation
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/ajms.2009.9.14
URL: https://scialert.net/abstract/?doi=ajms.2009.9.14
INTRODUCTION
11, 111, 1111 in base ten are not pure powers, we can easily verify it, but is it true for a number of n digits equal 1 in base ten, for all n. This study is an answer to this question. A number with n digits equal to 1 (111…1) in base ten is equal to a number with n digits equal to 9 (999…9) in base ten divided by 9, which means ![]() , the theorem stipulates that
, the theorem stipulates that ![]() ,
, ![]() . This research proposes an original and analytic proof of this theorem called Bugeaud and Mignotte theorem (Bugeaud and Mignotte, 1999).
. This research proposes an original and analytic proof of this theorem called Bugeaud and Mignotte theorem (Bugeaud and Mignotte, 1999).
THE PROOF
Let Bugeaud-Mignotte equation:
| Then with j2 = -1 |
| 10n-9Yq = 1 = 10n+j(9jYq) |
| We pose: |
| 10n = x, 9jYq = y, u = 1, z = 9jYq10n |
Lemma 1
(1) |
(2) |
Proof of Lemma 1
| And: |
| We pose: |
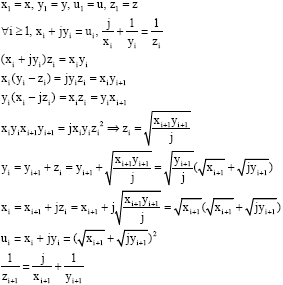 |
| until infinty. |
Lemma 2
| The expression of the sequences is |
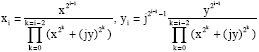 |
Proof of Lemma 2
| For I = 2, |
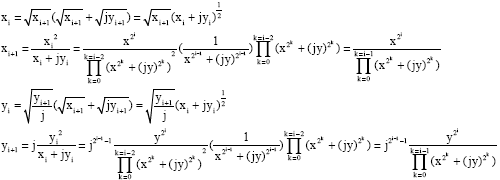 |
| But: |
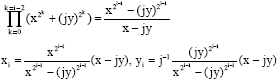 |
Lemma 3
xi-jyi = x-jy
Lemma 4
The lemmas 1, 2, 3 imply that jy-x = 0
Proof of Lemma 4
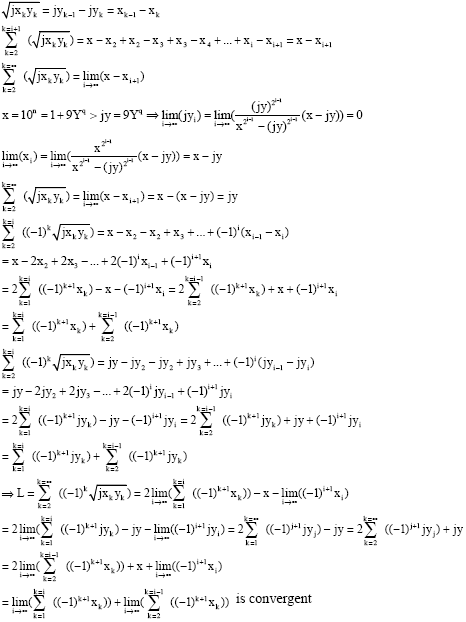 |
| We pose: |
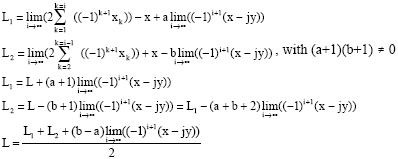 |
| We pose: |
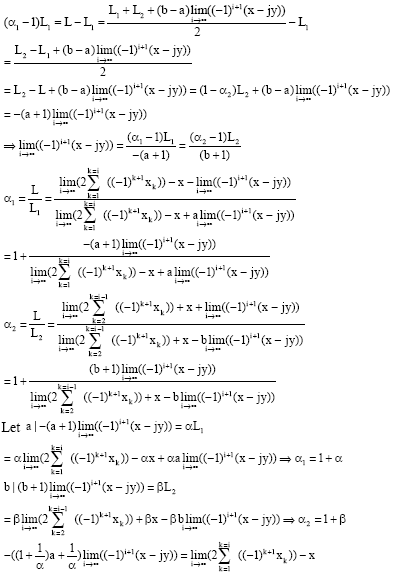 |
| And: |
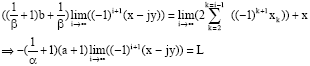 |
| And: |
| If we make the hypothesis that |
| And: |
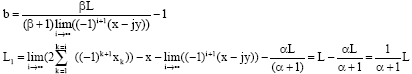 |
| But: |
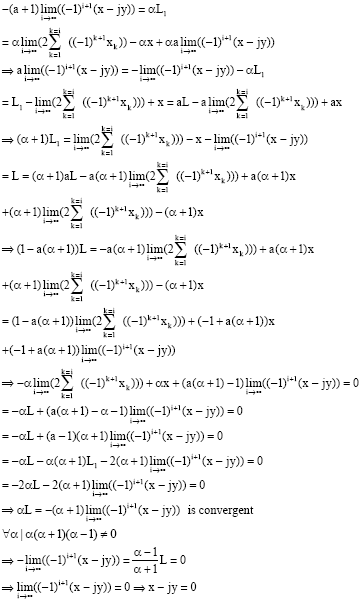 |
| The hypothesis |
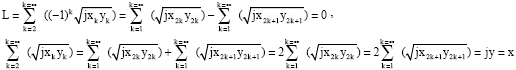 |
| In all cases |
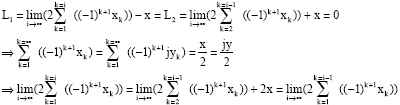 |
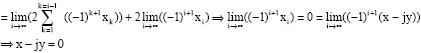 |
| And it is impossible: the existence of Y and q is impossible! |
CONCLUSION
Bugeaud-Mignotte equation has effectively no solution, and an analytic proof exists. The generalization is ![]() is it possible? It seems that there are only three solutions:
is it possible? It seems that there are only three solutions:
REFERENCES
- Bugeaud, Y. and M. Mignotte, 1999. Sur l'équation diophantienne xn-/x-1x-1 = yq, II = On the diophantine equation xn-1-x-1 = yq, II. Comptes Rendus de l'Académie des Sciences. Série 1, Mathématique, 328: 741-744.
Direct Link








