ABSTRACT
This study was motivated by the need to establish a vector form of autoregressive moving average (VARMA) models comprising linear and non linear components that could compete with the pure vector linear VARMA models. General bilinear vector autoregressive moving average (BIVARMA) was established as an extension of the univariate bilinear model. Three revenue series identified as autoregressive (AR) and Moving Average (MA) processes on the basis of the distribution of autocorrelation and partial autocorrelation functions were used to illustrate the performances of the two competing vector forms in terms of estimates and residual variances. Graphical comparisons were also made. The results showed that BIVARMA models established perform best and provide better estimates than the VARMA models.
PDF Abstract XML References Citation
How to cite this article
DOI: 10.3923/ajms.2009.33.40
URL: https://scialert.net/abstract/?doi=ajms.2009.33.40
INTRODUCTION
Most time series behave as though they have no fixed mean. Such series have arisen in forecasting and control problems, and all of them exhibit behavior suggestive of non stationarity.
Evidence of non linearity which is usually found in the dynamic behavior of such data implies that classical linear models are not appropriate for most time series. This called for the emergence of non-linear models in which bilinear forms a special class.
Maravall (1983) used a bilinear model to forecast Spanish monetary data and reported a near 10% improvement in one-step ahead mean square forecast errors over several autoregressive moving average (ARMA) alternatives. There is no doubt that most of the economic or financial data assume fluctuations due to certain factors.
On the contrary, Imeh (2007) observed that in certain time series applications, univariate linear estimates are comparatively better than those obtained from bilinear models.
Similar research engaged the attention of John (2008). He investigated the relative merits of multivariate linear process and univariate bilinear process using Canadian money and income data. The reports revealed that the linear models performed better than the bilinear models.
However, it is the objective of this study to establish a bilinear concept from a vector point of view and compare it performance with the vector linear model using a trivariate case of time series. That is, two multivariate cases of three vector elements each.
The general form of the bilinear model according to Granger and Anderson (1978) is given by:
| (1) |
Similarly, Rao (1981) described bilinear time series model BL (p, r, m, k) as given by the difference equation:
| (2) |
where, {e(t)} is an independent white noise process and C0 = 1. {X(t)} is termed the bilinear process. The autoregressive moving average model ARMA(p, r) is obtained from Eq. 2 by setting dll1 = 0 ∀ l and l1.
Parameter estimation of bilinear processes has been studied for particular cases by Bouzaachane et al. (2006) .
Boonchai and Eivind (2005) gave the general form of multivariate bilinear time series models as:
| (3) |
Here, the state X(t) and noise e(t) are n-vectors and the coefficients Ai, Mj and Bdij are n by n matrices. If all Bdij = 0, we have the class of well-known vector ARMA-models.
Iwok and Akpan (2007) established the matrix form of vector autoregressive time series as:
| (4) |
and recorded its advantages over the univariate case.
In this study, we are interested in the comparative performance of vector linear models and vector bilinear models. We considered three series of a vector and each was taken as response variable and the remaining two were lagged predictors. The data used for estimation are three sources of monthly generated revenue (for a period of ten years) from Ik. L.G.A. in Nigeria.
MATERIALS AND METHODS
Let Xlit be a vector of n-dimensional time series.
Linear Model
The general vector (VARMA) analogue to the univariate autoregressive moving average (ARMA) for the n-series is:
| (5) |
where, γk.ir and λl.it are the autoregressive (AR) and Moving Average (MA) parameters. p and q are the AR and MA orders. εlit [ε1i, ε2t, ..., εnt] is a vector of white noise. k and l represent the lags of AR and MA models.
is the vector AR part.
is the vector moving average part.
If λl.it = 0 for all lagged white noise, the linear vector AR (VAR) model can be isolated and written in the form:
| (6) |
Similarly, vector MA (VEMA) part can be obtained by setting γk.ir = 0 and the resulting expression is:
| (7) |
Vector Non Linear Models
Autoregressive (AR) Process
Given the vector elements X1t,X2t, ....., Xnt, the non linear model for an AR process is:
| (8) |
where, βkl.ir are the bilinear parameters of the product series and l = 0 ∀ q.
Moving Average (MA) Process
For the moving average process, the non linear model is expressed as:
| (9) |
where, βkl.ir are the bilinear parameters and k = 0 ∀ q.
Bilinear Vector Autoregressive-Moving Average Model (BIVARMA)
Combining Eq. 6-9, the BIVARMA model emerges:
| (10) |
Unlike Eq. 5, Eq. 10 comprises both the vector linear and vector non linear components. This study seeks to compare the performances of the two vector models (Linear and Bilinear).
RESULTS
Estimates for the VARMA Model
The distribution of partial autocorrelation function of the non stationary series suggested pure AR process of order 3 for X1t, AR process of order 2 for X2t and AR of order 1 for X3t. Similarly, autocorrelation function of the series suggested pure MA process of order 1 for X1t, MA process of order 1 for X1t and MA of order 2 for X3t. The regression estimates obtained provide the model below for the vector linear part.
| (11) |
where, γ1.il = 0.130, γ1.i2 = 0.235, γ1.i3 = 0.974, γ2.il = 0.224, γ2.i2 = 0.020, γ3.i1 = 0.196, λ1.il = 0.153, λ1.i2 = 0.153, λ1.i3 = 189, λ1.i3 = 242, λ2.i3 = 563.
Estimate for the BIVARMA Models
The bilinear vector autoregressive moving average model consists of two parts. The first part is the linear vector VARMA model, while the second part comprises the sum of the non linear components from AR and MA processes. The non linear part is product of lagged vector elements and white noise. Estimates of the BIVARMA parameters and fits were obtained by treating Eq. 10 as an intrinsically linear model. The following parameter estimates were obtained:
The regression estimates obtained produce the following models for the three vector elements:
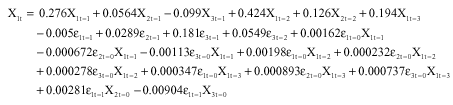 | (12) |
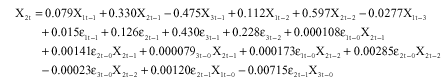 | (13) |
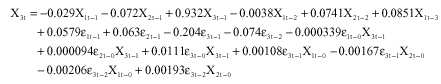 | (14) |
As could be seen above, these models are linear in states Xit-k but non-linear jointly with εit-1 as the name bilinear implies. The estimates provided by the above models are displayed in Table 2 and are found to be good, as evidenced by the closeness between the Actual and the estimated values.
Residual Variances
After fitting the models, the calculated residual variance from Eq. 11 is 81.19. Similarly, the residual variances for the bilinear vector models in Eq. 12-14 are 15.78 for X1t, 21.26 for X2t and 21.13 for X3t.Comparatively, the residual variances of the bilinear models are smaller than the variance obtained from the linear vector model. This makes bilinear vector ARMA models superior to the linear ARMA counter part.
Plots of Actual and Estimate Values
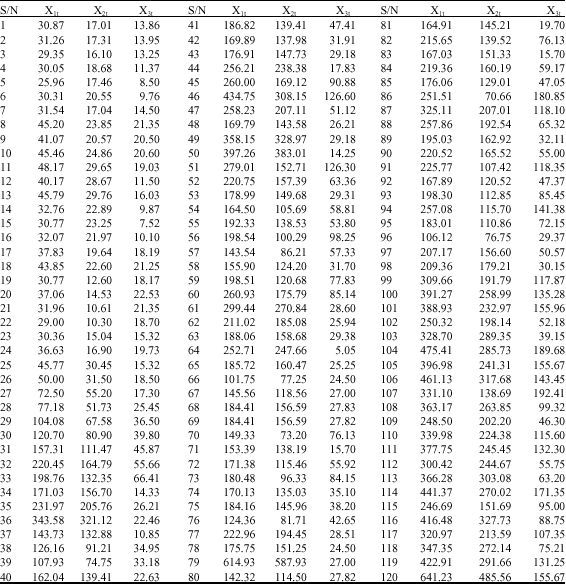
The actual and estimated values of our models presented in Table 1-3 are plotted in Fig. 1a, b-3a, b below. Each figure displayed contains two plots (the actual marked by o and the estimate marked by +).
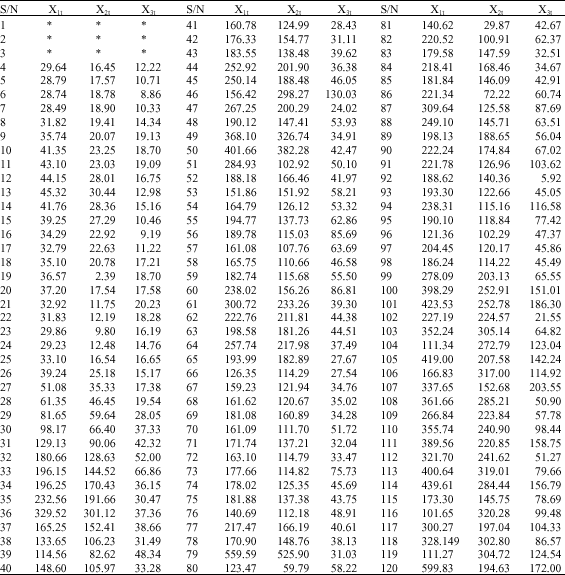
| Table 1: | Three sources of internal generated revenue (X1t,X2t,X3t) |
 | |
| Table 2: | BIVARMA Estimates of the generated revenues (X1t,X2t,X3t) |
 | |
| Table 3: | Estimates of the VARMA model |
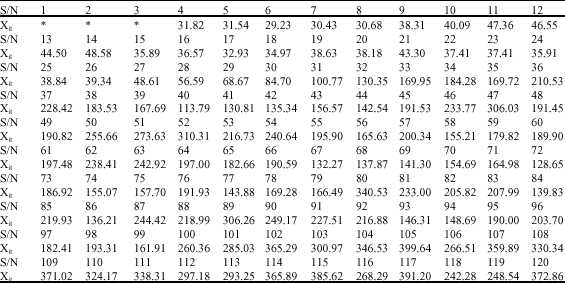 | |
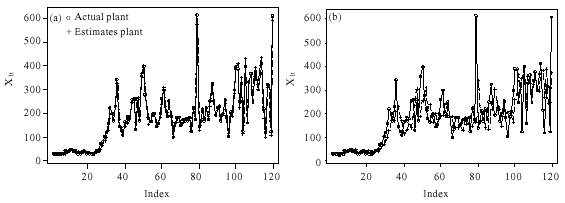 | |
| Fig. 1: | (a) Vector BILINEAR-ARMA and (b) Vector -ARMA Plots of actual and estimates of X1t |
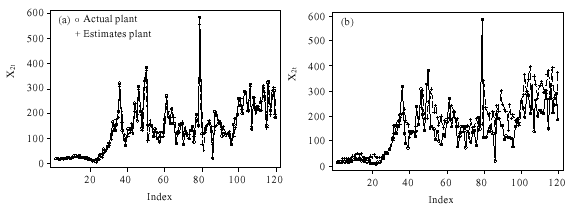 | |
| Fig. 2: | (a) Vector BILINEAR-ARMA and (b) Vector-ARMA Plots of actual and estimates of X2t |
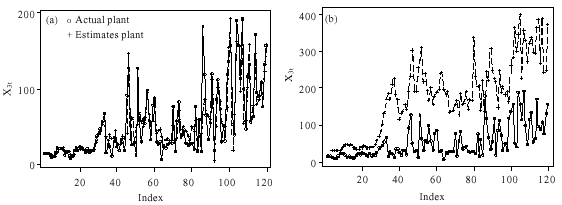 | |
| Fig. 3: | (a) Vector BILINEAR-ARMA and (b) Vector-ARMA Plots of actual and estimates of X3t |
The plots reveal that there is a strong marriage between the actual and the estimated values of the bilinear vector ARMA models. This is an indication of a high degree performance by the bilinear models. However, the great disparity in the actual and estimate plots of the pure vector ARMA model makes it inferior to bilinear models.
CONCLUSION
In essence, this study established the vector bilinear ARMA model and compared its performance with vector ARMA model. From the minimum variance property and graphical verdict shown, there is no gain saying the fact that some series especially, revenue series assume not only linear component but also non linear part. This is so because of the random nature of observations assume by certain processes. The result of this study confirms that non linear models such as bilinear vector ARMA are superior to pure linear vector ARMA models.
DISCUSSION
Through our practical illustrations in applying the vector bilinear models, we are led to believe that this new class of models offers exciting potential in the analysis of revenue data and opens up new vistas.
Comparatively, present result has contradicted the conclusions drawn by Imeh (2007) and John (2008). Whereas, Imeh (2007) and John (2008) emerged linear models as the best; this study is in support of Maravall (1983).
However, we have to note that this study utilized a vector bilinear approach as opposed to the univariate cases prioritized by the aforementioned authors; hence the difference in the respective outcomes.
Besides, we cannot ignore the fact that choice of data may also affect our results. Since present findings are restricted to economic time series data, evidence obtained here cannot be conclusive in general. Therefore we, suggest that this approach be extended to other cases, especially the modeling of hydrologic time series that are measured at short periods of time such as hourly or daily time intervals where the fitted stochastic models must take into account unique non linear properties of the data that are caused by complex physical processes.
REFERENCES
- Maravall, A., 1983. An application of non linear time series forecasting. J. Business Econ. Stat., 4: 66-74.
Direct Link - Rao, T.S., 1981. On the theory of bilinear time series models. J. R. Statist. Soc. Series B, 43: 244-255.
Direct Link








