Research Article
Conditional Dependence of Trivariate Generalized Pareto Distributions
Department of Academic, Laboratoire LANIBIO, UFR-SEA, Université de Ouagadougou, Burkina Faso
Extreme Values Theory (EVT) is based on modelling and measuring events which occur with very small probability. Mainly two methods have been developed in this theory: the block maxima method (Beirlant et al., 2005) and the Peacks-Over-Threshold (POT) approach (Coles, 2001; Resnick, 1987). The block maxima method is interested to asymptotic behavior of the laws of the component-wise maxima appropriately normalized under the condition that the univariate margins are independent and identically distributed (iid). This method shows that these asymptotic laws are the Multivariate Extreme Value Distributions (MEVDs). Suggested originally by hydrologists, the POT approach is rather based on modelling of exceedances of a random sample over a large threshold within a time period.
Earlier studies have developed statistical structures to describe the dependence of the multivariate distributions arising from these two approaches. In many latest books and reviews on the topic (Beirlant et al., 2005; Gaume, 2005), it has been shown that no single parametric family can summary the MEVDs like does do the Generalized Extreme Value (GEV) family in the univariate EVT. Nevertheless, if the univariate margins are given the dependence of these distributions can be characterized by equivalent measures like Pickands dependence function, exponent measure or stable tail dependence function (Degen, 2006). Furthermore, Tajvidi has shown (Tajvidi, 1996) that for a sample of random vectors ![]() the law H of the exceedances over a large threshold is the multivariate Generalized Pareto Distribution (GPD). Moreover, this excess distribution H is linked to the asymptotic component-wise maxima model G of the same sample by Eq. 1:
the law H of the exceedances over a large threshold is the multivariate Generalized Pareto Distribution (GPD). Moreover, this excess distribution H is linked to the asymptotic component-wise maxima model G of the same sample by Eq. 1:
| (1) |
The aim and particularity of this study is to build a new structure which describes the dependence of multivariate GPDs but under given conditions made on the marginal distributions. This new conditional dependence function enable us to characterize the basic parametric subfamilies of three-dimensional GPDs.
In this study, we consider the following problem: Let consider a situation where X = {(X1,...,Xn);n≥1} is a random vector with a multivariate GPD function H and we are interested to model a structure which describes both the dependence of H under the condition XI>x0,I and the dependence of the survival function ![]() of H under the condition XJ≤x0,J; x0,I and x0,J being given realizations of the complementary lower dimensional margins XI and XJ of X. Therefore, it is desirable to model the structure which gives at any realization x = (x1,...,xn) of X the probability of the discordances
of H under the condition XJ≤x0,J; x0,I and x0,J being given realizations of the complementary lower dimensional margins XI and XJ of X. Therefore, it is desirable to model the structure which gives at any realization x = (x1,...,xn) of X the probability of the discordances ![]() For this purpose Pickands dependence function of a MEVD would be useful (Coles, 2001; Beirlant et al., 2005). Let:
For this purpose Pickands dependence function of a MEVD would be useful (Coles, 2001; Beirlant et al., 2005). Let:
be the component-wise maxima of a random vector ![]() with univariate iid variables and with distribution function F. A m-dimensional continuous and non-degenerate function G is a MEVD if there exists vectors of normalizing sequences
with univariate iid variables and with distribution function F. A m-dimensional continuous and non-degenerate function G is a MEVD if there exists vectors of normalizing sequences ![]() with
with ![]() such that (in component-wise algebraic notations), for all
such that (in component-wise algebraic notations), for all ![]()
| (2) |
If Eq. 2 holds F is said to belong to the max-domain of attraction of G. Therefore, from the link established between G and H by Eq. 1, we obtain, for all x = (x1,...,xm)εIRm, the following characterization:
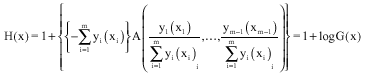 | (3) |
where, A is the Pickands dependence function of H defined on the unit simplex
in IRm-1 such that:
verifying for tεSm-1, the condition:
μ being the angular measure of H on Sm-1 (Beirlant et al., 2005). In addition, the yi are defined by the transformations:
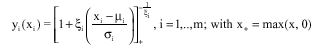 | (4) |
where, μiεIR. ξi. εIR and σi>0 are respectively the location, shape and scale parameters of the univariate margins Gi of G. The different values of the parameter ξi allow the GEV distribution defined by:
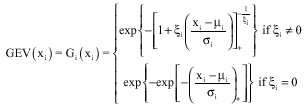 | (5) |
to describe the three types of asymptotic extreme behavior such as:
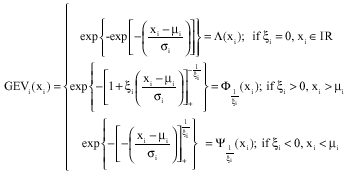 | (6) |
The laws Λ, Φ and Ψ are from Gumbel, Fréchet and Weibull, respectively.
Here, the main three theorems of this study will be presented and proved.
Angular Distribution of Multivariate GPDs
The following theorem gives the angular distribution of a multivariate GPD.
Theorem 1
Let H be a multivariate GPD. Then, there exists a function L(.) defined on Sm-1 in IRm-1 such as, for all x = (x1,...,xm)εIRm:
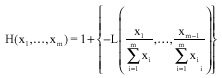 | (8) |
Moreover, if H is continuously differentiable of order m, the density function l of L fulfills, for all t = (t1,...,tm-1)εSm-1, the equality:
| (9) |
The function L(.) is the angular distribution of the multivariate GPD H.
Proof
Let V be the exponent measure function of the distribution H with unit Fréchet margins (Michel, 2006; Resnick, 1987). Therefore, for all xi>0 we have:
| (10) |
It is known that:
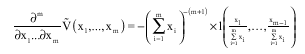 | (11) |
Where:
l(.) being the angular density of H. Furthermore, we have:
This result inserted in Eq. 11 gives :
By taking:
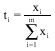 |
We have:
Replacing l(t1,...,tm-1) in Eq. 10 we see that Eq. 9 assertion holds.
For proving the following theorems we define a conditional dependence measure for the family of multivariate distributions.
A Conditional Measure of a Multivariate Distribution
Let n, k be natural numbers such that {n≥2;1≤k<n} and let Nk be a given subset of k elements of N = {1,...,n}, the set of the first n natural numbers.
Definition 1
We define Nk-partition of a random vector X ={(X1,...,Xn), n≥2} (or the partition of X in the direction of Nk) by the pairwise vector![]() as:
as:
| • | is the k-dimensional marginal vector of X whose component indexes are ordered in the subset Nk |
| • | is the (n-k)-dimensional marginal vector of X whose component indexes are ordered in |
| Similarly, every realization x = (x1,..,xn) of X can be decomposed into two parts |
are, respectively realizations of vectors ![]() et
et ![]() . If H, HNk and
. If H, HNk and ![]() denote the distribution functions of the random vectors
denote the distribution functions of the random vectors ![]() then for all realization x = (x1,...,xn) of X we have
then for all realization x = (x1,...,xn) of X we have
are the upper endpoints of the functions HNk and ![]()
Definition 2
Given a Nk-partition ![]() of X = (Xl,...,Xn) we define the upper Nk-discordance degree of X as the conditional probability given for all x = (xl,..., xn) εIRn by
of X = (Xl,...,Xn) we define the upper Nk-discordance degree of X as the conditional probability given for all x = (xl,..., xn) εIRn by ![]() Similarly, the lower Nk-discordance degree of X is defined, for all x = (xl,...,xn) in IRn by
Similarly, the lower Nk-discordance degree of X is defined, for all x = (xl,...,xn) in IRn by ![]() .
.
The following definition characterizes the probability that one of the margins ![]() and
and ![]() exceeds 1/2, while the values taken by the other are less than 1/2.
exceeds 1/2, while the values taken by the other are less than 1/2.
Definition 3
Given the distribution H of a multivariate random vector X = {(X1,...,Xn), n≥2} with univariate margins Hi, 1≤i≤n we define the upper Nk-median discordance degree of H by the real number denoted by : ![]() s quantile function of Hi. Similarly, the lower Nk-median discordance degree of H is defined by
s quantile function of Hi. Similarly, the lower Nk-median discordance degree of H is defined by ![]()
Example 1
Let X = (X1, X2, X3) be a trivariate random vector. Let’s consider N2 = {1, 3}. The lower N2-discordance degree of X is given, for x = (x1, x2, x3) ε IR3 by ![]() . Particularly, if H is a continuous distribution function of X we verify easily that
. Particularly, if H is a continuous distribution function of X we verify easily that ![]() , while for N1 = {1}, the upper N1-median discordance degree is given by
, while for N1 = {1}, the upper N1-median discordance degree is given by ![]() where H2>0 and H1,3>0 are, respectively the distribution functions of the margins X2 and (X1, X3);
where H2>0 and H1,3>0 are, respectively the distribution functions of the margins X2 and (X1, X3); ![]() being the inverse of the survival function of Hi. Let’s suppose, in addition that:
being the inverse of the survival function of Hi. Let’s suppose, in addition that:
for all xi ε]0,1] (distribution whose univariate margins are uniform on 0,1]), we check easily that, for θ = 1/2 we get :
The following result shows that the Nk-marginal distribution of a MEVD is also a MEVD.
Theorem 2
Suppose there exists a MEVD G describing the asymptotic behavior of the component-wise maxima of X suitably normalized. Then, there exists a k-dimensional MEVD Gk and a (n-k)-dimensional MEVD Gn-k associated, respectively to the component-wise maxima of the marginal vectors ![]() and
and ![]() Moreover Gk and Gn-k are the marginal distributions of G.
Moreover Gk and Gn-k are the marginal distributions of G.
Proof
Let σn = (σ1,...,σn)εIRn; σi>0 and μn = (μ1;...;μn) εIRn be the vectors of normalizing sequences of the component-wise maxima Mn = (M1,...,Mn) associated to the MEVD G by previous Eq. 2. Then, if
is the upper endpoint of marginal vector ![]() we have:
we have:
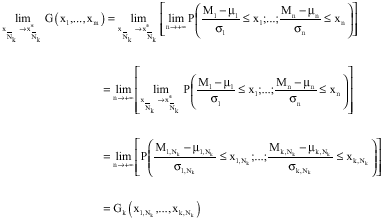 |
Therefore, there exists two vectors of normalizing sequences ![]() σi, Nk>0 and μNk = (μ1,Nk;...;μk, Nk) ε IRk such as the marginal component-wise maxima MNk = (M1, Nk,...,Mk,Nk) of Mn converges to GNk according to Eq. 2. Thereby Gk is a MEVD with k variables.
σi, Nk>0 and μNk = (μ1,Nk;...;μk, Nk) ε IRk such as the marginal component-wise maxima MNk = (M1, Nk,...,Mk,Nk) of Mn converges to GNk according to Eq. 2. Thereby Gk is a MEVD with k variables.
Similarly, we establish that Gn-k also arises as the limiting distribution of the marginal component-wise maxima ![]() linearly normalized with vectors of sequences
linearly normalized with vectors of sequences ![]() with
with ![]()
A Conditional Dependence Function of a Multivariate GPD
Note that, in the above, each of the discordance degrees ![]() and
and ![]() of a random vector X can be obtained by functional transformations of the other. Therefore, the following characterizations will be restricted to the upper
of a random vector X can be obtained by functional transformations of the other. Therefore, the following characterizations will be restricted to the upper ![]() which will be denoted by δ in the simplest case
which will be denoted by δ in the simplest case![]() i.e., k = 1.
i.e., k = 1.
Theorem 3
Let G be a MEVD with discordance degree δ. Then, there exists a convex function D defined on the unit simplex Sm-1 by:
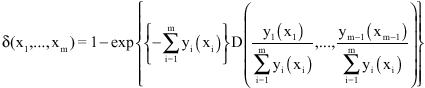 | (7) |
for all (x1,...,xm) in IRn ; where the yi(xi) satisfy Eq. 4, for i = 1,…, m.
D is called the discordance function of G or of its corresponding GPD H.
Taking a MEVD with unit Gumbel margin, Gi(xi) = exp{-exp(-xi)}; xi>0, the following corollary characterizes the simplest upper median degree, ![]() .
.
Corollary
Let G be a MEVD with unit Gumbel. Then, the upper median discordande degree of G, denoted by ![]() is given by
is given by
Example 2
Let Gθ, θ>1 be the logistic model of MEVD given for (x1, x2, x3)εIR3 by
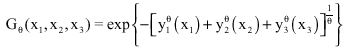 |
yi(xi) satisfying Eq. 4. Its discordance function is given, for all (t1, t2)εS2 by
and the median discordance degree
Particularly, for θ = 2, we get ![]() = 0.864.
= 0.864.
Proof of Theorem 3
Let's suppose that, for i = 1,…,m, the univariate margins Gi of the MEVD G have the generalized form: Gi(xi) = exp{-yi(xi)} where the yi (xi) satisfy Eq. 4. Therefore, for all (xl,...,xn)εIRn;
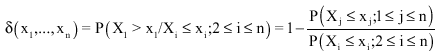 | (12) |
Thus, ![]() being the joint distribution of the margin vector (X2,...,Xn) of X, we have:
being the joint distribution of the margin vector (X2,...,Xn) of X, we have:
Furthermore, due to theorem 1, the function ![]() is a k-dimensional extreme value distribution. Therefore, if A and
is a k-dimensional extreme value distribution. Therefore, if A and ![]() are the Pickands dependence functions of G and
are the Pickands dependence functions of G and ![]() respectively, then, in Eq. 12 we have:
respectively, then, in Eq. 12 we have:
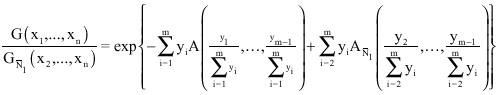 |
Furthermore, we have:
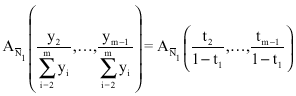 |
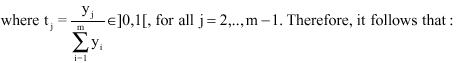 |
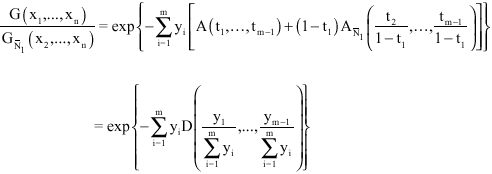 |
where, D is the convex function such that 0≤1-tl≤1 and defined on the unit simplex
by
 |
for all tεSm-1. Particularly for the trivariate case, we have:
defined on S2.
APPLICATION TO THE TRIVARIATE MODELS OF GPDs
The logistic model is the most important family of multivariate GPDs.
The Family of Trivariate GPD of Logistic Type
Let X = (X1, X2, X3) be a trivariate random vector with a parametric distribution Hθ, θ>1. The above Eq. 3 enable us to characterize Hθ by its discordance function Dθ via its Pickands dependence function Aθ (Michel, 2006).
Definition 4
The trivariate parametric function Hθ is a MGPD of Logistic Type if Hθ has, for all (x1, x2, x3)εIR3 the representation:
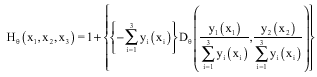 |
With the yi(xi) satisfying Eq. 4 and where the discordance function Dθ of Hθ is given for all:
We give here three basic trivariate GPDs of Logistic Type (Joe, 1997; Husler and Reiss, 1989) and we build their discordance functions:
| • | The trivariate family of GPD of Logistic Type of Gumbel |
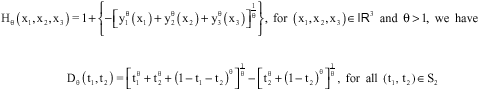 |
Particularly if θ→1¯ we obtain the trivariate Pareto independent model H(x1, x2, x3)=1+{-y1(x1) +y2(x2)+y3(x3)]} with D(t1, t2) = 2-t1 for (t1, t2)εS2
| • | The trivariate family of GPD of Logistic Type of Galambos |
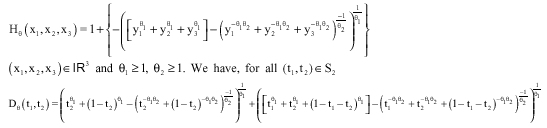 |
| • | The trivariate family of GPD of Logistic Type of Husler-Réiss |
The GPD which describes the behavior of the exceedances of the trivariate normal distribution over a large threshold is given for (x1, x2, x3)εIR3; θ = (θ1, θ2, θ3) by:
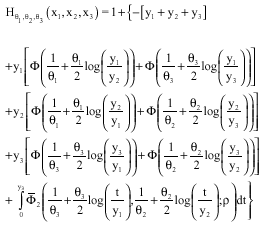 |
where, Φ notes the distribution function of the standard normal law and ![]() the survival function of the bivariate normal distribution function with covariance matrix:
the survival function of the bivariate normal distribution function with covariance matrix:
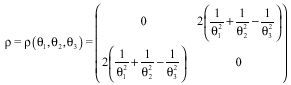 |
Thus, for all (t1, t2) the corresponding discordance function is:
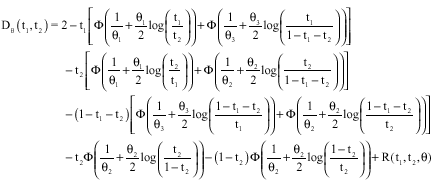 |
where, R(t1, t2, θ) is an integral rest defined for all (t1, t2)εS2.
The Family of Trivariate GPD of Nested Type
The Nested Logistic Type is an asymmetric subfamily of logistic model. It generalizes this model to allow different degrees of dependence between the components of the underlying random vector. For (x1, x2, x3)εIR3 and θ1, θ2>1, define now, recursively the following norm
where, ||.||θ is the usual θ-norm with the convention that the absolute value is taken if the norm does not have an index (Joe, 1997; Michel, 2006).
Definition 5
The distribution function given, for all (x1, x2, x3)εIR3, by
is called the generalized Pareto distribution of Nested logistic type.
The basic trivariate GPD of Nested Logistic Type is given, for θ1, θ2≥1 by:
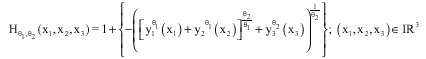 |
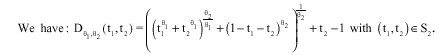 |
The Family of Trivariate GPD of Asymmetric Logistic Type
The asymmetric distributions arise as the models which describe the asymptotic behavior of the maxima of storms recorded at different locations along a coastline (Gaume, 2005). They generalize the logistic model but does not include the nested logistic model from the previous section (Michel, 2006).
Definition 6
Let B be a non-empty subset of {1,2,3} and let λC≥1 be arbitrary numbers for every C⊂B with |C|≥2 and λC = 1 if |C| = 1. Furthermore, let 0≤pi,C≤1 where, pi,C = 0 if I∉C and the side condition
is fulfilled for i=1,2,3. Then the distribution function
is a generalized Pareto distribution of Asymmetric Logistic Type.
The basic trivariate GPDs of Asymmetric Logistic Type with their discordance functions follow (Joe, 1997):
| • | The trivariate Asymmetric GPD of Logistic Type of Gumbel |
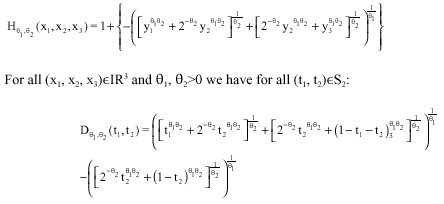 |
| • | The trivariate Asymmetric GPD of Logistic Type of Galambos |
 |
for (x1, x2, x3)εIR3 and θ1, θ2>0. We have, for (t1, t2), εS2
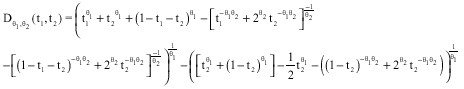 |
The results of the study show that the dependence of all trivariate GDP, under given conditions on the lower dimensional margins, is totally described by its discordance function. These results are similar to the characterizations of the multivariate GPDs developed by Tajvidi (1996) or to the equivalent dependence measures for MEVDs (Resnick, 1987; Beirlant et al., 2005). But the particularity of this study is the that the new measure and function describe the joint dependence under any condition made on the support of a lower dimensional margin. Moreover, the applications of the study determine clearly the three main subfamilies of the models of trivariate GPDs by characterizing them by their discordance function.
We found that the results conform to the solution of the problem considered earlier. This is seen at all realisations x = (xl,...,xn) of the random vector X. We also note that the theorem 3 establishes a link between the new dependence structure and the previous dependence measures via Pickands dependence one.
In this research we have investigated about characterization of a conditional dependence of multivariate families of generalized Pareto distributions. We have built a new measure and function which describe this conditional dependence. Basic trivariate subfamilies of multivariate GPDs have been characterized by this function. Moreover, we have computed the expressions of this function for the usual trivariate subfamilies of GPDs.