Research Article
An Approximate Likelihood Ratio Method for Testing Equality of Two Dependent Proportions
Department of Statistics and Demography, The National University of Lesotho, Kingdom of Lesotho
Dependent proportions are common in biomedical studies, such as studies that focus on changes in subjects’ responses over time, observations on severity of pain at pairs of body locations and retrospective case-control studies. Agresti (2002) describes several inference methods for such data. In a simple study involving a binary response, the data for dependent observations are displayed in a 2x2 contingency table, where, n11, n12, n21 and n22 denote, respectively, the number of pairs that are successes for both observations, successes for the first observation but failures for the second observation, failures for the first observation but successes for the second observation and failures for both observations. Commonly the four cell counts of the 2x2 contingency table are assumed to follow a multinomial distribution. Inferences about the parameters of the underlying distribution are based on the cell counts (Newcombe, 1998; Liu et al., 2002; Agresti and Min, 2005).
In the presence of non-response the individual cell counts are often difficult to obtain. A Bayesian approach described by Ghosh et al. (2000) could be used for dealing with problems of non-response if there is some auxiliary information. Suppose that we could not observe the nij due to the problem of non-response but the marginal totals are known. Assuming binomial distributions for the first row total and the first column total, the corresponding probabilities are:
Comparison of p1 and p2 is not straight forward because the subjects comprising the row and column counts are not independent. That is to say, if p1 is the proportion of patients who develop a specified type of complication and is the proportion of patients who develop a second type of complication, then the two proportions are not independent as some patients could exhibit both types of complications. Here, a bivariate probability distribution is proposed that accounts for the dependence of Y1 and Y2 . Using the joint distribution and the realized values y1 and y2, a likelihood ratio test is suggested for testing the equality of the two proportions.
LIKELIHOOD RATIO TEST
Bivariate Binomial Distribution
Suppose different discrete events, which are naturally related, are observed simultaneously. There are a number of multivariate distributions that could be used to model such events. The problem is that a bivariate distribution which is of a binomial type and which allows for dependence is not readily available. If the two random variables satisfy the Poisson assumptions, then one could use the bivariate Poisson distribution introduced by Kocherlakota and Kocherlakota (1992). It reads as:
(1) |
The resulting marginal distributions of Y1 and Y2 are Poisson with parameters λ and μ, respectively. The correlation of Y1 and Y2 is assumed to be positive. The parameter α (>0) represents the correlation of Y1 and Y2. The higher α, the stronger the correlation. If α is high, the probability that each of the variables takes on a large value yj is higher than the probability that one of them takes on a small value and the other one a large value. That is to say, the two variables are highly concordant.
Suppose that two positively correlated binomial random variables Y1 and Y2 are assumed to follow a bivariate distribution where the probability P(Y1 = y1, Y2 = y2) increases by some factor as the correlation increases. The following distribution could be assumed in this case:
(2) |
where, y1 and y2 taking values 0, 1, . . . , n.
The factor K does not depend on y1 and y2 as it is used to normalize the distribution, that is, to make the summation over all y1 and y2 equal 1. When the two random variables are independent, or α = 1, the joint distribution (Eq. 1) reduces to a product of two binomial distributions. The main problem is that it is not clear whether or not we can get a binomial marginal distribution from the above bivariate distribution. However, since the objective is to test the equality of the two proportions using a likelihood ratio test, it is reasonable to expect the resulting likelihood ratio statistic to provide a valid comparison unless the actual values of α in the numerator and denominator of the likelihood ratio are much larger than 1.
Approximation of the Likelihood Ratio Statistic
A test for comparing the two probabilities of success is describes here using the bivariate binomial distribution introduced above.
Given n and the realized values y1 and y2 , the objective is to test:
In an ordinary likelihood ratio test one would take the logarithm of the joint probability (Eq. 1) and maximize it with respect to the parameters p1, p2 and under H0 and H1 separately. Direct maximization is not possible because the factor K in Eq. 1 also depends on the parameters. Instead one could try to identify an optimal point (p1*, p2*) in the neighborhood of (y1/n, y2/n) for specified values of α. The likely range for α is expected to be small (i.e., 1 to 2, or 1 to 3). As α increases the value of K decreases and as a result the likelihood function starts to decline. Therefore, it is sufficient to try values of α such as 1.1, 1.2, …, 3 and then refine the search once the likely range is identified. The resulting optimal values , p1*, p2* and α* are taken as the likelihood estimates under H1.
A similar search procedure is used to identify p0 = p1 = p2 and α0 that maximize the likelihood function under H0. If the optimal value of is saved for each pair p1 and p2 during the search for p1*, p2* and α* then one could simply look for the optimal among points where p1 = p2.
Finally, the estimates are substituted for p1, p2 and α in the likelihood function to get l* and l0, the maximized log-likelihood under H1 and H0 , respectively. The resulting approximate likelihood-ratio statistic is defined as:
(3) |
where, H0 is true G2 is assumed to follow a chi-square distribution with 1 degree of freedom for large n.
The test is, therefore, to reject the null hypothesis when G2 is higher than χ12 at specified level of significance. The basic S-plus commands for finding the optimal values of p1, p2, α and the corresponding value of the likelihood are shown in the Appendix.
| Appendix |
 |
| } # xval is a matrix of the estimates, each row contains p1, p2, the corresponding optimal and the value of the likelihood function when the parameters take on these values. |
EXAMPLE
From the records of TB patients treated at a tuberculosis treatment center in Lesotho, Southern Africa, a sample of 30 TB patients was selected. Fourteen of the patients had improper follow-up (not being assigned an observer, non-compliance, controlled tests not done as prescribed, treatment taking longer than 6 months, etc.). Five of the patients either died or failed to respond to the treatment. The objective is to test whether there is a significant difference between the proportion of patients who had improper follow-up and the proportion of patients who died or failed to respond to treatment.
Suppose Y1 and Y2 denote the number of patients in a sample of size 30 that exhibit the respective outcomes. Therefore, in the notations of the preceding sections, n = 30, y1 = 14 and y2 = 5. Following the procedure described earlier it is assumed that the distribution of Y1 and Y2 is bivariate binomial introduced earlier. To speed up the identification of optimal points, the normalizing factor is found as follows:
That is,
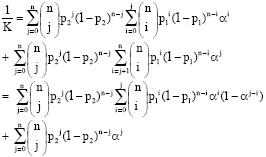 |
This value is substituted for K in the likelihood when the algorithm is used to identify the optimal point.
The test of interest is
Since, y1/n =14/30 = 0.47, y2/n =5/30 = 0.17, it is sufficient to search for p1 in 0.11 to 0.65 and for p2 in 0.05 to 0.39. Then choose evenly spaced points within the two ranges of values with 0.02 as spacing value. Initially the value of α was made to vary in [1, 4] using 0.1 as spacing value. After observing that, the likelihood started to decline for all possible points (p1,p2) when α exceeded 2.5, the refined search is restricted to this range with spacing value of 0.02. The optimal values under the null hypothesis were p1 = p2 = 0.35 and α = 1.08 and the resulting log-likelihood was -6.50229. Under the alternative hypothesis p1 = 0. 43, p2 = 0.19 and α = 1.14 with log-likelihood of -3.5791. This resulted in an approximate likelihood-ratio statistic G2 = -2(-3.5791-(-6.50229)) = 5.846, which has a p-value of 0.01 assuming a chi-square distribution with 1 degree of freedom. Since, the p-value is small, there is a strong evidence to conclude that the proportion of patients who received improper follow-up and the proportion of patients who died or failed to respond to the treatment are not equivalent.
In the study, an approximate likelihood-ratio test is proposed for comparing two dependent proportions. Unlike the standard analysis, the procedure uses only the marginal totals of the contingency table, which makes it useful for dealing with non-response. The algorithms presented in the study can also be applied for comparing pairs of such proportions in terms of the strength of their correlation.
The main advantage of the proposed test is that it does not require sophisticated computation adopted by other procedures for making inference when the data have problems of non-response. The procedures used in the test are simple and can be applied without requiring extensive re-sampling methods.
Although, no attempt was made in the study to see the comparative performance of the proposed test procedure, the mathematical arguments and computation of the test statistic are simple and straightforward. Regarding the power of the test, it is clear that no theoretical significance is placed on the distribution adopted for the test statistic. However, as the test statistic resembles a likelihood-ratio statistic, the power of the test is expected to be comparable to that of techniques that employ re-sampling or Monte Carlo estimation to handle non-response problems.