Research Article
Detecting Non-linearity Using Squares of Time Series Data
Department of Mathematical and Physical Sciences, Michael Okpara University of Agriculture, Umudike, P.M.B. 7267, Umuahia, Abia State, Nigeria
According to Granger and Andersen (1978) bilinear models are formed by adding a bilinear form to the autoregressive/moving average (ARMA) models leading to
(1) |
where {et} is a sequence of i.i.d random variables with zero mean and finite variance ![]() and et is independent of Xs, s<t. The formal difference between a bilinear time series model and an ARMA model is the bilinear term eX.
and et is independent of Xs, s<t. The formal difference between a bilinear time series model and an ARMA model is the bilinear term eX.
Bilinear models were first studied in the context of non-linear control systems, but their application as time series model were investigated principally by Granger and Andersen (1978) and Subba Rao (1981). Following Subba Rao (1981) we represent (1) as BL (p, q, m, k) where BL is abbreviation for bilinear. Subba Rao et al. (1984) also gives a comprehensive account of this class of models. Sessay and Subba Rao (1988, 1991), Akamanan et al. (1986), Gabr (1988), Subba Rao and Silva (1993) and many other authors have examined various simple forms of (1) in the context of stationarity, invertibility and estimation.
The motivation for using data values to detect non-linearity is provided by a result inherent in the work of Granger and Newbold (1976). They showed that for a series {Xt} which is normal (and therefore linear)
σk (X2t) = [σk(Xt)]2 |
where σk (.) denotes the lag k autocorrelation. Any departures from this result presumably would indicate a degree of non linearity, a fact pointed out by Granger and Andersen (1978).
Granger and Andersen (1978), have also shown that for single term bilinear time series {Xt} satisfying
Xt = bXt-1 et-k + et |
(![]() ) has the same covariance structure as an ARMA (1,k) process.
) has the same covariance structure as an ARMA (1,k) process.
We show below that for the pure diagonal bilinear process (![]() ) would have the same covariance structure as an ARMA (p,p) process.
) would have the same covariance structure as an ARMA (p,p) process.
Properties of Squares of PDBL Model
Now consider the pure diagonal bilinear model satisfying
(2) |
where {et} is a sequence of i.i.d random variables with zero mean and constant variance ![]() .
.
Let Wt = ![]()
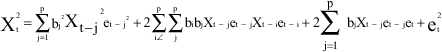 | (3) |
We are going to consider three cases namely: k<p, k = p and k>p where k is the lag of the autocovariance coefficient.
Case 1: k<p
It can be shown that
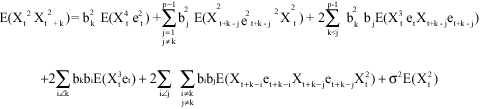 | (4) |
But, the autocovariance function of a stationary process {Xt} is given by
R(k) = E(Xt-μ) (Xt+k -μ) = E(XtXt+k) -μ2. Therefore, Rw(k) = E (WtWt+k) -μ2w |
where Rw (k) is the autocovariance function of Wt = Xt2 at lag k and μw = E(Xt2). Therefore,
(5) |
Case 2: k = p
It can easily be shown that:
and
Therefore,
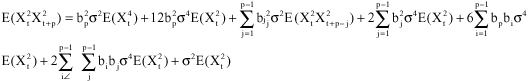 | (6) |
Substituting for ![]() in (4) and simplifying we obtain
in (4) and simplifying we obtain
(7) |
Observe that this is a Yule-Walker type difference equation.
Case 3: k>p
In this case, it can easily be shown that
(8) |
Substituting for ![]() in (4) and simplifying, we obtain
in (4) and simplifying, we obtain
(9) |
This is the Yule-Walker equation for an ARMA (P,P) model. Present study on squares of Xt satisfying (1) leads to the following theorem needed for identification purposes.
Theorem 1
Let {et} be a sequence of independent and identically distributed random variables with E(et) = 0
![]() Suppose there exists a stationary and invertible process {Xt} satisfying
Suppose there exists a stationary and invertible process {Xt} satisfying
for some constants b1,b2,...bp, p>0. Then ![]() will be an ARMA (P,P) model.
will be an ARMA (P,P) model.
COMPARISON WITH A LINEAR MODEL
Here it is shown that if {Xt} is MA (P), then { ![]() } is also MA (P). We proceed as follows:-
} is also MA (P). We proceed as follows:-
For the MA (P) model
Then
It is easy to show that the following are true:
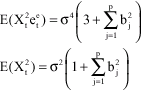 |
and
We proceed to treat the autocovariance as follows
CASE 1: k≤p
For k<p, it can be shown that
 |
Taking expectation, we have
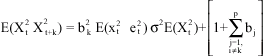 |
Substituting in Eq. 5, we have that
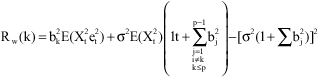 |
CASE 2: k>p
We recall that
and
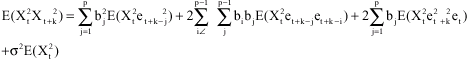 |
Thus
Hence ![]() is also an MA (P).
is also an MA (P).
SIMULATION RESULTS
Here we present some simulation to illustrate the results obtained in this study. In what follows, the random variable {et} are mutually independent and identically distributed as N(0,σ2). The processes considered are:
Xt = 0.7Xt-1et-1 + et | (10) |
Yt = 0.7+ et+ 0.146et-1 | (11) |
The simulation and estimation were done using MINITAB. For purposes of illustration, we have without loss of generality taken σ2 = 1 for (10) and (11). We generated for each process 200 observations (X1, X2,...X200). The autocorrelation for Xt,,yt and were estimated.
The estimator
rk = R(k)/R(0), k = 1,2,3,...
was used to estimate the autocorrelation, where
is the estimate of the autocovariance R(k) and
is the estimate of the mean.
| Table 1: | Showing Estimated Autocorrelation for Xt, X2t, yt and y2t |
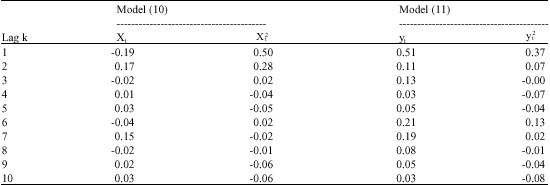 | |
As these estimators have been discussed in detail by Chatfield (1980) they have just been stated here. The parameters have been carefully chosen to ensure the invertibility and stationarity of the processes. Table 1 gives the estimated autocorrelation of the models (10) and (11) and their squares.
Xt is seen to identify as an MA (1) under covariance analysis and at least as ARIMA (1,1) as the theory predicted. Both yt and would identify as no more than MA (1). Therefore, looking at the square of a series is a useful way of distinguishing between a linear and a bilinear model having the same covariance analysis properties.
One way of distinguishing between linear and non-linear models is to perform a second-order analysis on the squares of the series. Some authors have shown that for a series {Xt} which is normal (and therefore linear)
(12) |
where σk (.) denotes the lag k autocorrelation. Any departures from this result presumably would indicate a degree of non-linearity, a fact pointed out by Granger and Andersen (1978).
We have, however, shown in this paper that this result (12) does not hold for the pure diagonal bilinear model. We have shown that the covariance structure of the square of a moving sequence time series is the same as the covariance structure of the original series. And this result can be used to distinguish between a pure diagonal and a linear model.