Research Article
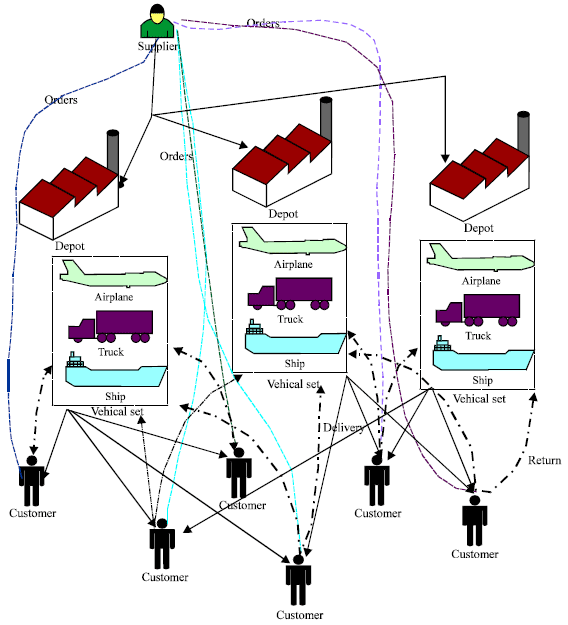
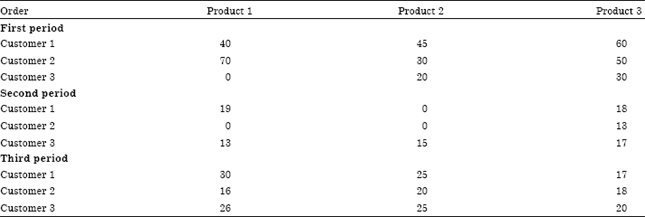
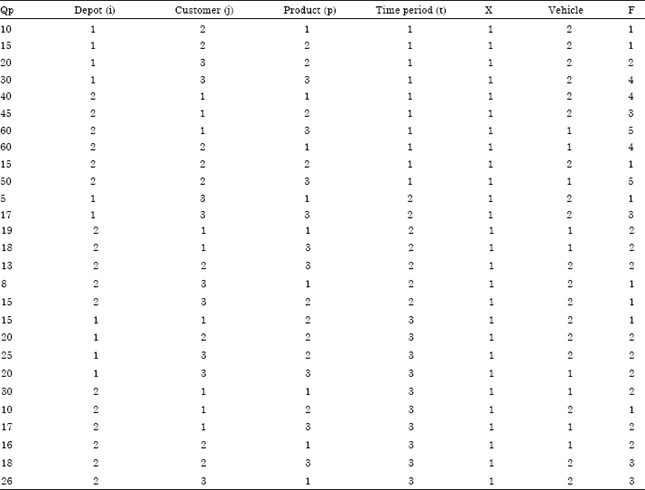
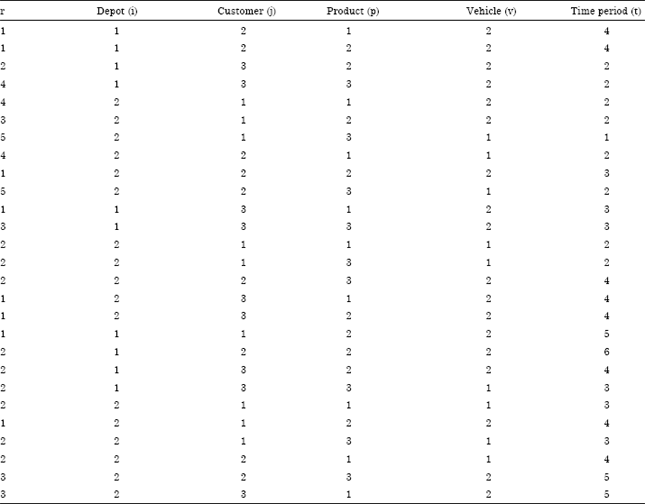
A Mathematical Model for Vehicle Routing Problem in a Flexible Supply Network
Faculty of Industrial Engineering, Iran University of Science and Technology, Tehran, Iran
Iraj Mahdavi
Department of Industrial Engineering, Mazandaran University of Science and Technology, Babol, Iran
Nezam Mahdavi-Amiri
Faculty of Mathematical Sciences, Sharif University of Technology, Tehran, Iran
Amir Mohajeri
Department of Industrial Engineering, Mazandaran University of Science and Technology, Babol, Iran















Yajba Sook Reply
How can I get hold of the LINGO code for this problem?
Miguel Angel Walle Reply
How can I get hold of the LINGO code for this problem?