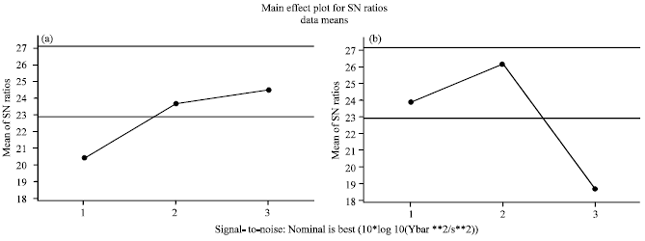
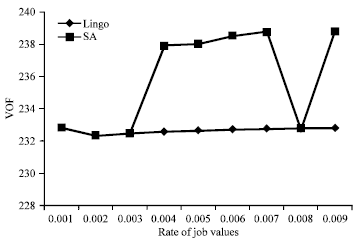
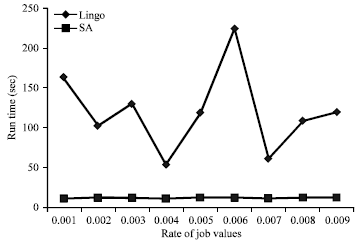
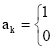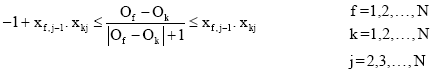Research Article
A Simulated Annealing for the Single Machine Batch Scheduling with Deterioration and Precedence Constraints
Department of Industrial Engineering, Iran University of Science and Technology, Narmak, Tehran, Iran
Hamidreza Haddad
Department of Industrial Engineering, Iran University of Science and Technology, Narmak, Tehran, Iran
Payam Ghanbari
Department of Industrial Engineering, Iran University of Science and Technology, Narmak, Tehran, Iran