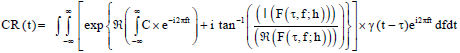Research Article
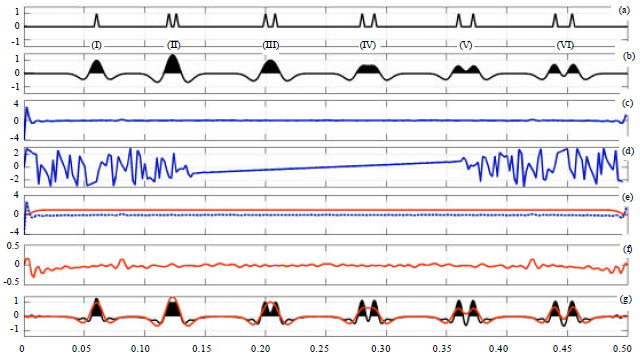
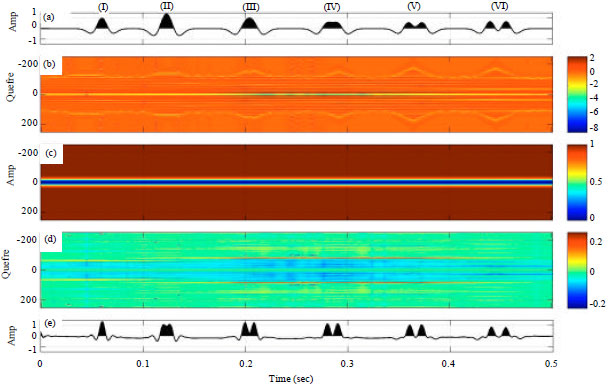
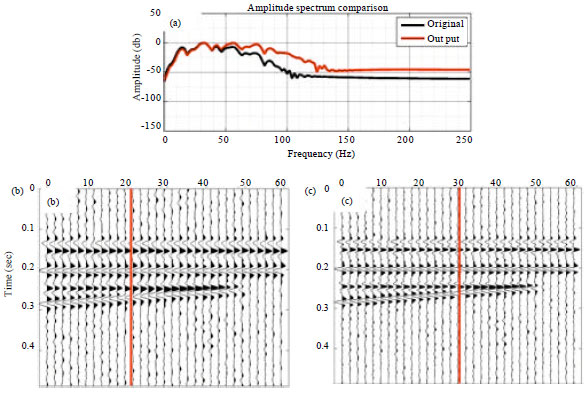
Increasing the Robustness of Homomorphic Deconvolution for Non-stationary Seismic Wavelet
Department of Geoscience and Petroleum Engineering, Universiti Teknologi PETRONAS, Malaysia
D.P. Ghosh
Department of Geoscience and Petroleum Engineering, Universiti Teknologi PETRONAS, Malaysia