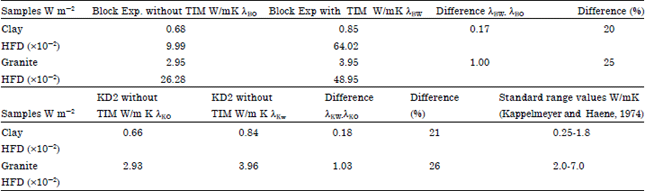
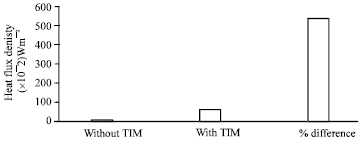
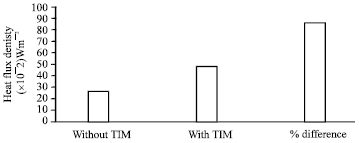
Research Article
Improved Determination of Heat Flux Density in Porous Media Using Modified Block Method
Department of Physics, University of Agriculture, PMB 2240, Abeokuta, Nigeria
Yemi S. Onifade
Department of Physics, Federal University of Petroleum Resources, Effurun, Nigeria
Biodun S. Badmus
Department of Physics, University of Agriculture, PMB 2240, Abeokuta, Nigeria