ABSTRACT
The propagation of Love waves in presence of a horizontal rigid barrier of finite length in the surface layer has been discussed. The transmitted waves have been obtained by using Wiener-Hopf technique and Fourier transform. The numerical computation has been done by assuming depth of barrier small as compared to the wavelength of the incident wave. It has been observed that the transmitted waves decrease as the distance from the barrier increases and die out after a very long time. The result of semi-infinite barrier has been obtained as a special case of this problem.
PDF Abstract XML References Citation
How to cite this article
URL: https://scialert.net/abstract/?doi=ajes.2012.1.12
INTRODUCTION
The problems concerning the propagation of seismic waves through crustal layer of earth have been of considerable importance for seismologists since a long time. Such type of study helps the scientists in understanding the internal structure of earth, which in turn can be used for exploration of valuable materials like oil, hydrocarbons, minerals etc. The problems of propagation of Love waves in different media have been discussed by Deshwal and Mudgal (1998), Kar et al. (1986), Niazy and Kazi (1980), Wong et al. (1995) and Singh (1998). Jardaneh (2004) has considered the expected source of earthquake evaluating the ground source response spectra taking into account local soil properties to evaluate seismic forces. Kaur et al. (2005) have studied the reflection and refraction of SH-waves at a corrugated interface between two laterally and vertically heterogeneous viscoelastic solid half-space. Dhaimat and Dhaisat (2006) have studied the sharp cut decrease of Dead Sea. The propagation of wave in inhomogeneous thin film has been discussed by Ugwu et al. (2007) using the series expansion solution method of Green’s function. Tomar and Kaur (2007) have studied the problem of reflection and transmission of a plane SH-wave at a corrugated interface between a dry sandy half space and an anisotropic elastic half space. They used the Rayleigh method of approximation for studying the effect of sandiness, the anisotropy, the frequency and the angle of incidence on the reflection and transmission coefficients. Ademeso (2009) has discussed the deformation traits in Charnockitic rocks by analyzing the direction of maximum compressional and tensional stresses inferred from the rose diagram. Chattopadhyay et al. (2009) has studied the reflection of shear waves in viscoelastic medium at parabolic irregularity. The authors found that the amplitude of reflected wave decreases with increasing length of notch and increases with increasing depth of irregularity. The finite element method analysis has been used by Adedeji and Ige (2011) to investigate and compare the performance of a reinforce concrete bare frame infilled with or without straw bale wall shape memory alloy diagonal wires subjected to seismic loads and earthquake ground excitation. Ramli and Dawood (2011) have studied the effect of steel fibers on the engineering performance of concrete. A computational technique has been applied to study the field propagation through an inhomogeneous thin film using Lippmann-Schwinger equation by Ugwu (2011). The propagation of seismic waves has also been studied by Zaman (2001), Hai-Ming and Xiao-Fei (2003), Balideh et al. (2009) and Aziz et al. (2011). The problem of Love wave excitation due to interaction between ocean wave and sea bottom topography gas been studied by Saito (2010). Here, we discuss the propagation of Love waves through irregularity in form of an infinite rigid strip present in the surface layer.
This study is based on a paper by Sato (1961) who studied the problem of reflection and transmission of Love waves in case the surface layer is variable in thickness. Here we discuss the propagation of Love waves through irregularity in form of a finite rigid horizontal barrier present in the surface layer at finite depth.
THE PROBLEM AND ITS SOLUTION
The propagation of Love waves due to a finite rigid horizontal barrier in the surface layer has been discussed in the present paper. The problem is being analyzed in zx-plane. The z-axis has been taken vertically downwards and x-axis along the interface. The Love wave is normally incident from right to left on a perfectly rigid screen -l<x<0; z = -h. The geometry of the problem is shown in Fig. 1. The incident Love wave is given by:
| (1) |
| (2) |
Where:
| (3) |
and C1N is the phase velocity of nth mode and k1N is the root of equation:
| (4) |
μ1 and μ2 being the rigidities of shear waves in the half space and in the crustal layer, respectively.
The wave equation in two dimensions is given as:
| (5) |
The wave equation in the present study for the surface layer can be written as:
| (6) |
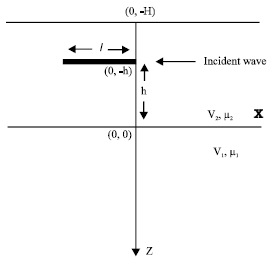 | |
| Fig. 1: | Geometry of the problem |
Where:
| (7) |
V1 and V2 are the velocities of shear waves in the half space z≥0 and in the layer -H≤z≤0, respectively.
Let the total displacement be given by:
| (8) |
| (9) |
| (10) |
The boundary conditions are:
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
The boundary conditions (11) and (12) specify that the barrier is rigid and no displacement takes place across the barrier. Using boundary conditions (11) and (12), we have:
| (16) |
| (17) |
Taking Fourier transform of Eq. 6, we obtain:
| (18) |
where, ![]() represents Fourier transform of vj (x, z)which can be defined as:
represents Fourier transform of vj (x, z)which can be defined as:
 | (19) |
If for a given z, as|x|→ ∞ and M,τ>0, |vj (x, z)| ~ Me-τ|x|, then ![]() + (p, z) is analytic in β>-τ and
+ (p, z) is analytic in β>-τ and ![]() - (p, z) is analytic in β<τ (= Im (kj)). So by analytic continuation
- (p, z) is analytic in β<τ (= Im (kj)). So by analytic continuation![]() (p, z) and its derivatives are analytic in the strip -τ<β<τ in the complex p-plane. Solving Eq. 18 and choosing the sign of θj such that its real part is always positive, we obtain:
(p, z) and its derivatives are analytic in the strip -τ<β<τ in the complex p-plane. Solving Eq. 18 and choosing the sign of θj such that its real part is always positive, we obtain:
| (20) |
| (21) |
Solving Eq. 21 by using boundary condition (15), we get:
| (22) |
Differentiating above equation with respect to z and putting z = -h and denoting ![]() , (p, -h) by
, (p, -h) by ![]() , (p) etc. and then eliminating A (p), we obtain:
, (p) etc. and then eliminating A (p), we obtain:
| (23) |
Solving Eq. 18 for j = 3, using boundary condition (13), we have
| (24) |
Differentiating above equation with respect to z and putting z = -h and denoting ![]() , (p, -h) by
, (p, -h) by ![]() , (p) etc. and then eliminating D (p) we obtain:
, (p) etc. and then eliminating D (p) we obtain:
| (25) |
where, δ = H-h.
Taking Fourier transformation of Eq. 14:
| (26) |
From Eq. 16 and 17, we can write in usual notation as:
| (27) |
Now using Eq. 26 and 27 in Eq. 25 for z = -h we have:
| (28) |
Now from Eq. 23 and 28 for z = -h, we can write:
| (29) |
Where:
| (30) |
| (31) |
The Eq. 29 is the Wiener-Hopf type differential equation discussed by Noble (1958).
SOLUTION OF WIENER-HOPF EQUATION
Now using Eq. 27 and 29 may be written as:
| (32) |
Where:
| (33) |
Now we factorize ![]() as discussed by Sato (1961) as:
as discussed by Sato (1961) as:
| (34) |
Let p = ± k1m and p = ±k2m are the zeros of f1 (p) and f2 (p), respectively. Then we write:
| (35) |
Where:
| (36) |
and G1 (p)and G2 (p) have no zeros. Also we can write:
| (37) |
Where:
| (38) |
Where:
| (39) |
| (40) |
tan φ2 and tan n2 are obtained from Eq. 39 and 40 by replacing H by h.
Now, we write:
| (41) |
Where:
| (42) |
and |K+ (p)|→|p|1/2, as |p|→ ∞.
Now ![]() can be factorized as:
can be factorized as:
| (43) |
Using Eq. 34 and 43, Eq. 32 can be written as:
| (44) |
Where:
| (45) |
Similarly, Eq. 34 may also be written as:
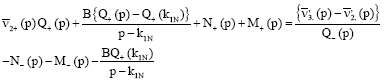 | (46) |
Where:
| (47) |
and:
| (48) |
Also, multiplying Eq. 32 by eipl and rearranging the terms, we have:
| (49) |
Where:
| (50) |
and:
| (51) |
Also, we make following substitutions for simplicity:
| (52) |
Where:
| (53) |
and:
| (54) |
Now Eq. 23 and 25 may respectively be written as:
| (55) |
and:
| (56) |
Where:
 | (57) |
The displacement v2 (x, z) is obtained by inversion of Fourier transform of Eq. 55 as given below:
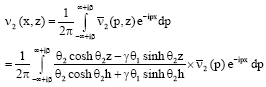 | (58) |
Also, the displacement v3 (x, z) is obtained by inversion of Fourier transform of Eq. 56 as given below:
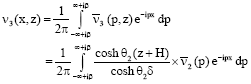 | (59) |
where, ![]() (p) is given in Eq. 57.
(p) is given in Eq. 57.
RESULTS AND DISCUSSION
For finding different component of waves, we evaluate the integral in Eq. 58 and Eq. 59 in different regions. For evaluation of Eq. 58, as anticipated, there is a pole at p = k1N having no contribution. Furthermore, let p = k2m be the roots of Eq. f2 (p) = θ2 cosh θ2h+γθ1 sinh θ2h = 0. The residue due to this pole contribute to:
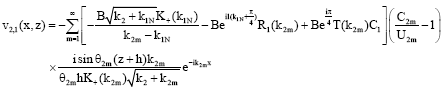 | (60) |
where, ![]()
Equation 60 represents the transmitted waves in the region -h≤z≤0; -l≤x≤0. The first term in this equation represents the component of diffracted wave at the edge x = 0, while other terms are the interaction terms due to second edge. Similarly, the pole at p = k1m contributes to:
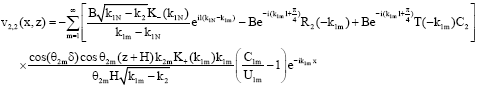 | (61) |
The Eq. 61 represents the transmitted waves in the region -h≤z≤0, -∞≤x≤-l and the first term represents the diffracted component of waves at the edge x = -l.
Also:
and:
are the phase velocities of Love type waves of mth mode in the layered structure with a layer of uniform thickness h.
Now we find the transmitted waves in the region -H≤z≤-h; x≤0. There is a pole at p = k1N, the contribution due to which is zero. The poles at:
n = 1, 2, 3...., contributes to:
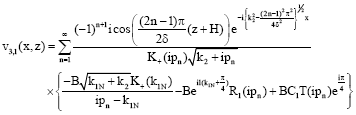 | (62) |
Equation 62 represents the transmitted waves in the region -H≤z≤-h; -l≤x≤0. The poles at p = k2m contributes to:
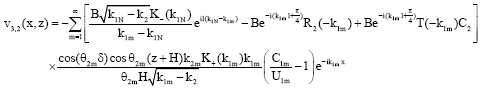 | (63) |
Equation 63 represents the transmitted waves in the region -H≤z≤-h; -∞≤x≤-l. Clearly, this result is an analytic continuation of the result obtained in Eq. 61.
NUMERICAL COMPUTATION AND ANALYSIS OF RESULTS
The transmitted waves in different regions have been found out in Eq. 60, 61, 62 and 63. For computation purpose we have considered k2δ small as compared to the wavelength of the incident Love waves. We have taken, V1 = 4.6 km sec-1, V2 = 3.9 km sec-1, μ1 = 7.98x1010 pa, μ2 = 4.11x1010 pa, k2δ<0.01 for calculation purpose and different waves have been obtained. In the present discussion, we have taken the barrier of finite length. As a limiting case of this problem, if we take l→ ∞ , then we have only one edge at x = 0 and Eq. 60 will have only the first term, which is same as obtained by Kazi (1975) for a semi-infinite barrier. Also, if we take l = 0, i.e., the whole of the surface layer is rigid, the Love wave moves with the velocity of shear waves in the surface layer.
CONCLUSIONS
We studied the problem of propagation of Love waves in the layered media with a surface layer having a horizontal rigid barrier of finite length. The numerical computation shows that the diffracted Love wave decreases as the distance from the barrier increases. It is clear from the discussion that if the barrier of large size is considered, the diffracted wave of larger intensity is observed. So by measuring the component of the wave obtained, the internal structure of earth can be predicted for specific study. The case of semi-infinite barrier is obtained as a special case.
REFERENCES
- Adedeji, A.A. and S.P. Ige, 2011. Comparative study of seismic analysis for reinforced concrete frame infilled with masonry and shape memory alloy wire. Trends Applied Sci. Res., 6: 426-437.
CrossRef - Ademeso, O.A., 2009. Deformation traits in the charnockitic rocks of akure area, Southwestern Nigeria. Asian J. Earth Sci., 2: 113-120.
CrossRefDirect Link - Aziz, Z.A., D.L.C. Ching and F.S. Yousif, 2011. Scattering of p-wave in fluid saturated medium. Trends Applied Sci. Res., 6: 710-718.
CrossRefDirect Link - Balideh, S., K. Goshtasbi, H. Aghababaei, N. Khaji and H. Merzai, 2009. Seismic analysis of underground spaces to propagation of seismic waves (case study: Masjed soleiman dam cavern). J. Applied Sci., 9: 1615-1627.
CrossRefDirect Link - Chattopadhyay, A., S. Gupta, V.K. Sharma and P. Kumari, 2009. Propagation of shear waves in visco-elastic medium at irregular boundaries. Acta Geophysica, 58: 195-214.
Direct Link - Deshwal, P.S. and S. Mudgal, 1998. Scattering of Love waves due to the presence of a rigid barrier of finite depth in the crustal layer of earth. Proc. Ind. Acad. Sci., 108: 81-94.
Direct Link - Dhaimat, O. and S. Dhaisat, 2006. Study of sharp-cut decrease of dead sea. J. Applied Sci., 6: 211-216.
CrossRefDirect Link - Jardaneh, I.G., 2004. Evaluation of ground response due to earthquakes-case study. J. Applied Sci., 4: 364-368.
CrossRefDirect Link - Kaur, J., S.K. Tomar and V.P. Kaushik, 2005. Reflection and refraction of SH-waves at a corrugated interface between two laterally and vertically heterogeneous viscoelastic solid half-spaces. Int. J. Solid Struct., 42: 3621-3643.
CrossRefDirect Link - Kazi, M.H., 1975. Diffraction of Love waves by perfectly rigid and perfectly weak half plane. Bull. Seism. Soc. Am., 65: 1461-1479.
Direct Link - Niazy, A. and M.H. Kazi, 1980. On the Love wave scattering problem for welded layered quarter-spaces with applications. Bull. Seis. Soc. Am., 70: 2071-2095.
Direct Link - Ramli, M. and E.T. Dawood, 2011. Effect of steel fibers on the engineering performance of concrete. Asian J. Applied Sci., 4: 97-100.
CrossRefDirect Link - Saito, T., 2010. Love wave excitation due to the interaction between a propagating ocean wave and the sea bottom topography. Geophys. J. Int., 182: 1515-1523.
CrossRef - Tomar, S.K. and J. Kaur, 2007. SH-waves at a corrugated interface between a dry sandy half-space and an anisotropic elastic half space. Acta Mechanica, 190: 1-28.
Direct Link - Ugwu, E.I., 2011. Computational method of studying the field propagation through an inhomogeneous thin film medium using lippmhhann-schwinger equation. Trends Applied Sci. Res., 6: 73-80.
CrossRefDirect Link - Ugwu, E.I., P.C. Uduh and G.A. Agbo, 2007. The effect of change in refractive index on wave propagation through (FeS2) thin film. J. Applied Sci., 7: 570-574.
CrossRefDirect Link - Singh, S.J., 1998. On attenuation of Love waves in a two layered half space. Wave Motion, 28: 191-193.
CrossRefDirect Link - Zaman, F.D., 2001. Diffraction of SH-waves across a mixed boundary in a plate. Mech. Res. Comm., 28: 171-178.
CrossRef - Hai-Ming, Z. and C. Xiao-Fei, 2003. Studies on seismic waves. Acta Seismologica Sinica, 16: 492-502.
CrossRef








