Research Article
Symmetry of Hamiltonian Systems
Department of Mathematics, University of Rajasthan, Jaipur, India
P. Sharma
Department of Mathematics, University of Rajasthan, Jaipur, India
The use of differential form in mechanics and its eventual formulation in terms of symplectic manifolds has been slowly evolving since Cartan (1922). The first modern exposition of Hamiltonian systems on symplectic manifolds seems to be due to Reeb (1952).
In this study the Hamiltonian systems formalism given in Abraham and Marsden (1978) and Arnold (1989) is used to derive the equations of motion for a particle on a line with a spring force and for a free particle in n-space from the energy function and the kinetics of the phase space.
The study of symmetry provides one of the most appealing applications of group theory. Groups were first invented to analyze symmetries of certain algebraic structures called field extensions and because symmetry is a common phenomenon in all sciences, it is still one of the two main ways in which group theory is applied the other way is through group representations. One can study the symmetry of plane figures in terms of groups of rigid motions of the plane. Plane figures provide a rich source of examples and a background for the general concept of group operations. Plane figures have generally bilateral symmetry, rotational symmetry, translational symmetry, glide symmetry and their combination.
HAMILTONIAN SYSTEM
A general Hamiltonian system consists of a manifold X, possibly infinite dimensional together with a (weakly) non-degenerate closed two-form ω on X (i.e., ω is an alternating bilinear form on each tangent space TxX of X, dω = 0 and for xεX, ωx (u, v) = 0 for all uεTxX implies v = 0) and a Hamiltonian function H: X→ú. Then X, H, ω determine in nice cases, a vector field XH called the Hamiltonian vector field determined by the condition:
| (1) |
Flows
Let X be a smooth manifold. A C∞-function F:![]() is called a flow for the vector field v if Fx:
is called a flow for the vector field v if Fx: ![]() →X is an integral solution for v i.e.,
→X is an integral solution for v i.e.,
or
and
Hamiltonian Flow
Let (X, H, ω) be a Hamiltonian system. A flow F is called a Hamiltonian flow if it preserves the symplectic form and the Hamiltonian function (i.e., Ft* ω = ω and Ft*H = H for tε![]() ) (Abraham and Marsden, 1978).
) (Abraham and Marsden, 1978).
Group Actions
Let G be a group and let X be a set. An action of G on X is an assignment of a function Sg: X→X to each element gεG such that:
| • | If I is the identity element of the group G, then SI is the identity map, i.e., for any xεX we have SI (x) = x |
| • | For any g, hεG we have SgοSh = Sgh, i.e., for every xεXwe have Sg(Sh (x)) = Sgh (x) |
A Lie-group action should satisfy certain differentiability properties in addition to the algebraic properties given above. The action is called effective if Sg = Identity map for only t = 0.
SYMMETRY OF HAMILTONIAN SYSTEMS
The symmetry of Hamiltonian system (X, ω, H) is a function S: X→X that preserves both the symplectic form ω and the Hamiltonian function H.
Motion of a Particle on a Line in the Plane with the Spring Force
The phase space of such a physical system Simmons (1991) is the simplest non-trivial symplectic manifold, the two-dimensional plane X = R2 = {(q, p): qεR, pεR} with the area two-form ω = dq∧dp.
The Hamiltonian function for such a particle is:
| (2) |
where, second term in the Hamiltonian is the potential energy of the spring.
Using the Eq. 1, we have for qεR and vεTqR
Taking
and
as an arbitrary vector field. We find:
or
or
and
Thus we have:
since, ∂/∂q and ∂/∂p are functions of time t (along a particular trajectory) we can write the vector field:
as time derivative along trajectories on the plane, since ∂/∂q and ∂/∂p are linearly independent we have:
| (3) |
which shows that equation of motion for a particle in a line with spring force is a linear differential equation:
| (4) |
We can draw the useful picture by using the conservation of the Hamiltonian by the Hamiltonian flow because it implies that the orbits of the system must lie inside level sets of H (An orbit is set of all points in phase space that the system must passes through during one particular motion. In other words it is the set of all points on one particular trajectory). The beautiful features of Hamiltonian systems is that we can get information about orbits of the differential equations of motion by solving the algebraic equation H = constant, which is easy to solve. So, here first we determine the Hamiltonian flow of the spring problem.
HAMILTONIAN FLOW OF THE SPRING PROBLEM
For finding the bona fide solutions to our differential equations, i.e., not only the orbit of a trajectory but the trajectory itself (i.e., the position as a function of time). We use the algebraic equation H0 = constant to reduce our original system of differential equations:
into one scalar differential equation:
| (5) |
which on integration gives:
| (6) |
The Hamiltonian flow for the linear differential Eq. 4 is given by the function:
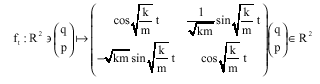 | (7) |
or
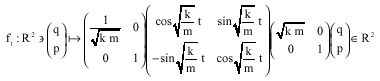 | (8) |
Geometrically, the flow at time t in phase space is effected by first scaling the q-axis by a factor of ![]() , which takes the orbits to circles, second, rotating these circles clockwise through an angle
, which takes the orbits to circles, second, rotating these circles clockwise through an angle ![]() and finally rescaling the q-axis back to its original scale. Since, for each t the function ft is a linear function from R2to R2 and because the determinant of the matrix representing ft is 1, ft is area preserving. So, the flow preserves the symplectic form.
and finally rescaling the q-axis back to its original scale. Since, for each t the function ft is a linear function from R2to R2 and because the determinant of the matrix representing ft is 1, ft is area preserving. So, the flow preserves the symplectic form.
Also the Hamiltonian flow preserves the Hamiltonian for ft* H = H, i.e., Hοft, we have, for gεSO(2), (special orthogonal group):
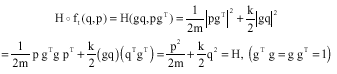 |
the level sets of H in phase space are ellipses (Fig. 1),
Here if k is large the ellipses are tall and skinny, while if k is close to 0 then the ellipses are short and wide. If k = 1/m the ellipses degenerate to circles. As the flow preserves the Hamiltonian, each solution of the system must lie entirely with in one ellipse in phase space. The conservation of the Hamiltonian by the Hamiltonian flow tells us that orbits must lie inside sets of the form ![]() . Since the motion is continuous, it follows that each orbit is contained in the curve
. Since the motion is continuous, it follows that each orbit is contained in the curve![]() (Fig. 1):
(Fig. 1):
The spring Hamiltonian given in Eq. 2 is an action of the group (R, +) on R2, for:
| • |
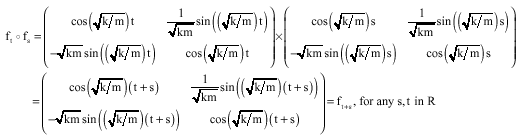 |
 | |
| Fig. 1: | Phase space of the particle on the line with level sets of the spring Hamiltonian |
This action is not effective because if t is an integer multiple of ![]() then:
then:
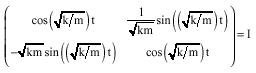 |
Which also shows that the flow is periodic with period ![]() .
.
MOTION OF A FREE PARTICLE IN n-SPACE
Consider the motion of a free particle in n space. Let q = (q1, ..., qn) be the position vector of the particle and p = (p1, ..., pn) be the corresponding momentum vector of the particle. Then the phase space of the particle is the manifold ![]() with the symplectic form:
with the symplectic form:
and the Hamiltonian function
Then ω, H determine the vector field XH by the condition (1)
Let ![]() be arbitrary vector fields, then using (1), we have:
be arbitrary vector fields, then using (1), we have:
or
This gives;
ai = pi/m and bi = 0, (i=1,…,n).
Thus the vector field is given by:
| (9) |
Taking the vector field:
| (10) |
as time derivative along trajectories, we have:
| (11) |
This gives:
| (12) |
the required equation of motion of the free particle in n- space
HAMILTONIAN FLOW OF THE PARTICLE IN n-SPACE
The Hamiltonian flow of the Particle in n-space is determined by taking the algebraic equation:
| (13) |
with the system of differential equations (1.9.3) and initial condition p(t) = p(0), t = 0, we have:
| (14) |
Thus for any fixed time t, the map:
defined by:
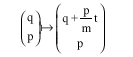 | (15) |
is a Hamiltonian flow, for:
and ft* H = H.
To show that every flow is not a Hamiltonian flow. If we take the flow of the problem particle in n-space as:
defined by:
| (16) |
for any ![]() hus gt is not a Hamiltonian flow of a Hamiltonian system with the canonical symplectic form on
hus gt is not a Hamiltonian flow of a Hamiltonian system with the canonical symplectic form on ![]()
Taking ![]() as the symplectic form on
as the symplectic form on ![]() then the flow gt defined Eq. 16 preserves ω, for:
then the flow gt defined Eq. 16 preserves ω, for:
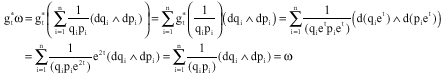 |
The Hamiltonian function for this system can be determined by taking
and
as arbitrary vector fields, then Eq. 1, we have:
or
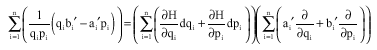 |
which gives:
which on integration yields:
| (17) |
Now:
Hence, gt preserves H. Thus gt defined Eq. 16 is a Hamiltonian flow for the Hamiltonian system (M, ω, H), where,
M = ![]() 2n-{0}
2n-{0}
and H is given Eq. 17.
The Hamiltonian flow of the Particle in n-space given Eq. 15 can be written as:
 |
and satisfying the condition of group action, for:
| • | 0εR, f0 is indeed an identity matrix |
| • |
The action is also effective. Thus the time flows of the Spring problem and Particle in n-space problem are symmetry of Hamiltonian system. But a Hamiltonian system may have other type of symmetries in addition to the time flow. For the problem the phase space of such a particle motion is:
with symplectic form ![]() and the Hamiltonian function
and the Hamiltonian function ![]() . Consider the translation action of the group (Rn, +) on X, for each g = (g1, ..., gn) in Rn, define the function:
. Consider the translation action of the group (Rn, +) on X, for each g = (g1, ..., gn) in Rn, define the function:
by
| (18) |
Then Sg is the symmetry of the Hamiltonian system for any gεRn, for:
and Sg* H =H.
Since, Sg gives a one-to-one correspondence from X to X, shows that Sg preserves the symplectic manifold.
Next, consider the rotational symmetry of a free particle in n-space.
The Hamiltonian system for such a particle is:
The action of SO(n) on X is defined by Sg(p, q) = (gq, pgT) and is called the rotation action. Here, Sg preserves manifold X and symplectic form, since, g is constant and an orthogonal matrix g gT, also we have:
and Sg* H = H, i.e., HοSg = H, for:
Hence, the action of the Lie group (Rn, +) on :
preserves both the symplectic form and the Hamiltonian function called the translation and rotation symmetry of the mechanical system. These symmetries are linear symmetries so they can express in matrix form.
In this study we have shown that every flow is not Hamiltonian but by changing the symplectic form and with some restriction on the phase space one can successfully change the non Hamiltonian flow into the Hamiltonian flow. Also, we have discussed the symmetry group properties of the mechanical system. For two body problem only these symmetries are sufficient for consideration but for other system nonlinear symmetries also arise (for further discussion about symmetry of differential equations and Hamiltonian systems see Artin (1991) and Marsden and Ratiu (1999)). The above symmetries of a mechanical system are useful in reducing the phase space of the system using the Marsden-Weinstein theorem.