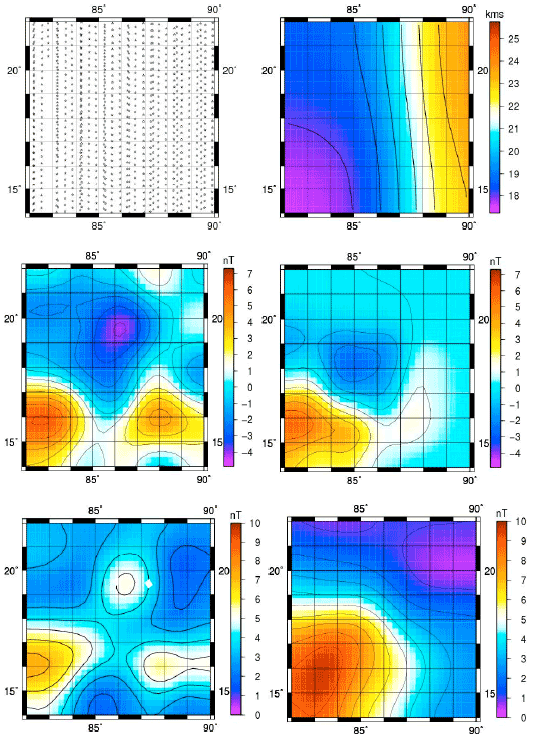
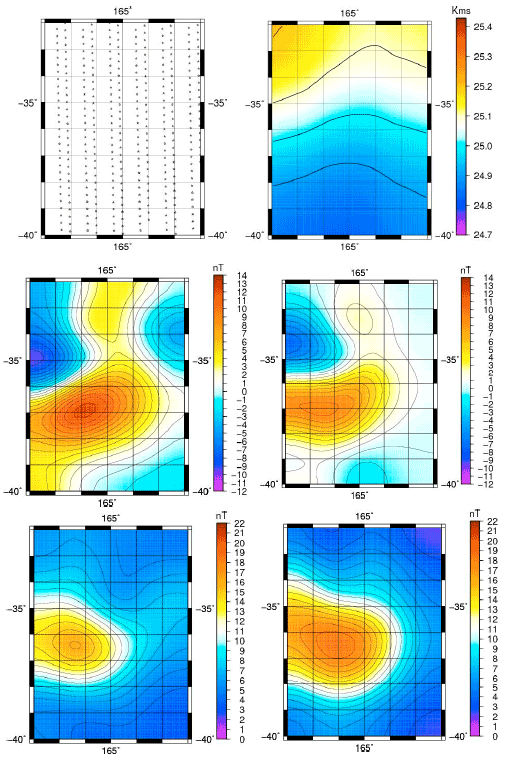
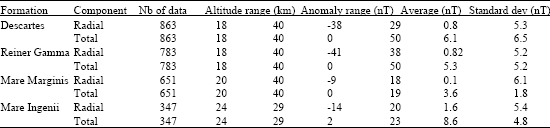
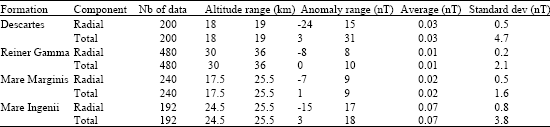
Research Article
Lunar Magnetic Pole Positions Deduced from High Albedo Magnetic Anomalies
Institut de Physique du Globe de Paris, CNRS 4, Place jussieu 75005 Paris, France
M. Hamoudi
Institut de Physique du Globe de Paris, CNRS 4, Place jussieu 75005 Paris, France
Y. Cohen
Institut de Physique du Globe de Paris, CNRS 4, Place jussieu 75005 Paris, France
E. Thebault
Institut de Physique du Globe de Paris, CNRS 4, Place jussieu 75005 Paris, France