Research Article
Forecasting the Garlic Production in Bangladesh by ARIMA Model
Department of Statistics, Jahangirnagar University, Savar, Dhaka, 1342, Bangladesh
Faruq Abdulla
Department of Statistics, Islamic University, Kushtia, 7003, Bangladesh
Garlic (Allium sativum L.) has been used in world cuisines as well as in herbal medicine for thousands of years and at times, has been claimed to help prevent everything from high cholesterol to cancer (Rahman et al., 2012). Among the species grown in Bangladesh, garlic is undoubtedly one of the important crops cultivated during cool season. It has been in use for many centuries and was recognized for its therapeutic and medicinal value as far back as the era of ancient Egypt. It is a common ingredient in the preparation of meals in all parts of the world, used for its pungent flavour. The most common use of garlic in the preparation of cooked dishes is in the form of fresh cloves. However, there are many preparations of garlic available, particularly in health food stores, including powdered garlic, tablets and oil capsules. In order to elucidate the role of garlic in the prevention of atherosclerosis, a large number of studies have investigated its effects on serum cholesterol, Low-Density Lipoprotein (LDL) cholesterol, High-Density Lipoprotein (HDL) cholesterol and triglycerides (TG) (El-Sabban and Abouazra, 2008). Garlic juice reduced serum cholesterol and TG in human subjects (Bakhsh and Chughtai, 1984) and helped in preventing the rise of serum cholesterol, thus indicating a cholesterol-lowering property (Beier, 1990; Zink and Chaffin, 1998).
A systematic review of randomized controlled trials in humans reported that the reduction of total cholesterol and TG with garlic therapy was evident after 1 month and persisted for at least 6 months (Silagy and Neil, 1994). A meta-analysis of controlled trials on fresh garlic showed that consuming half a clove per day decreased total serum cholesterol levels (Warshafsky et al., 1993).
A controlled trial and a meta-analysis of the use of garlic powder in the treatment of moderate hyperlipidaemia showed that it was less effective in reducing total cholesterol (Berthold and Sudhop, 1988). A meta-analysis of 13 trials showed that garlic tablets significantly reduced total blood cholesterol levels (Stevinson et al., 2000).
Garlic has been considered as a rich source of carbohydrates, proteins and phosphorus (Bose and Som, 1990). Garlic also helps eliminating waste materials and dangerous free radicals from the human body (Durak et al., 2004). Garlic is profitable crop on the basis of its return to investment. Among the competitive crops like mustard, groundnut and cabbage, the highest net return was obtained from garlic cultivation, human labour, land preparation cost, manure, TSP, irrigation and insecticide had positive effect on the yield of garlic. Non-availability of HYV seed at proper time, lack of technical knowledge, infestation of insects and diseases and low market price were the major problems of garlic cultivation (Haque et al., 2013). Garlic is generally cultivated with traditional method. Though, production of garlic is increasing day by day, but in a land of hungry country like Bangladesh, it may not be possible to meet the domestic demand due to increase in population. Moreover, the production of garlic is insufficient in Bangladesh. Every year, Bangladesh imports big amounts of garlic from neighboring country and others to meet up the demand of its population. To meet the demand of domestic consumption of garlic, it is too much essential to estimate the production of garlic in Bangladesh which leads us to do this research. The main purpose of this research is to identify the Auto-Regressive Integrated Moving Average (ARIMA) model that could be used to forecast the production of garlic in Bangladesh.
Data source: This study considered the published secondary data of yearly garlic production in Bangladesh, which was collected over the period 1971-2013 from the website of FAOSTAT.
ARIMA model: Suppose that {ζt} is a white noise with mean zero variance σ2, then {Yt} is defined by Yt = ζt+β1ζt-1+β2ζt-2+...+βqζt-q is called a moving average process of order q and is denoted by MA(q). If the process {Yt} is given by Yt = α1Yt-1+α2Yt-2+...+αpYt-p+ζt is called an auto-regressive process of order p and is denoted by AR (p). Models that are combination of AR and MA models are known as ARMA models. An ARMA (p, q) model is defined as Yt = α1Yt-1+α2Yt-2+...+αpYt-p+ζt+ β1ζt-1+β2ζt-2+...+βqζt-q, where, Yt is the original series, for every t, we assume that ζt is independent of Yt-1, Yt-2,..., Yt-p. A time series (Yt) is said to follow an integrated autoregressive moving average (ARIMA) model if the dth difference Wt = ∇dYt is a stationary ARMA process. If {Wt} follows an ARMA (p, q) model, we say that (Yt) is an ARMA (p, d, q) process. Fortunately, for practical purposes, we can usually take d = 1 or at most 2. Consider then an ARIMA (p, 1, q) process, with Wt = Yt-Yt-1, we have, Wt = α1Wt-1+α2Wt-2+...+αpWt-p+ζt+β1ζt-1+β2ζt-2+...+βqζt-q.
Box-jenkins method: The influential work of Box-Jenkins (Box and Jenkins, 1970) shifted professional attention away from the stationary serially correlated deviations from deterministic trend paradigm toward the ARIMA (p, d, q) paradigm. It is popular because it can handle any series, stationary or not with or without seasonal elements.
The basic steps in the Box-Jenkins methodology consist of the following five steps:
| • | Preliminary analysis: Create conditions such that the data at hand can be considered as the realization of a stationary stochastic process |
| • | Identification of a tentative model: Specify the orders p, d, q of the ARIMA model so that it is clear the number of parameters to estimate. Empirical auto-correlation functions play an extremely important role to recognize the model |
| • | Estimation of the model: The next step is the estimation of the tentative ARIMA model identified in step 2. By maximum likelihood method we estimate the parameters of the model |
| • | Diagnostic checking: Check if the model is a good one using tests on the parameters and residuals of the model |
| • | Forecasting: If the model passes the diagnostics step, then it can be used to interpret a phenomenon, forecast |
Ljung-box test: Ljung-Box (Ljung and Box, 1978) test can be used to check auto-correlation among the residuals. If a model fit well, the residuals should not be correlated and the correlation should be small. In this case the null hypothesis is H0: ρ1 (e) = … = ρk (e) is tested with the Box-Ljung statistic:
where, N is the no of observation used to estimate the model. This statistic Q* approximately follows the chi-square distribution with (k-q) df, where q is the no of parameter should be estimated in the model. If Q* is large (significantly large from zero), it is said that the residuals auto-correlation are as a set are significantly different from zero and random shocks of estimated model are probably auto-correlated. So, one should then consider reformulating the model.
Evaluation of forecast error: Before performing growth analysis it is necessary to estimate the growth model that best fits the time series. There are many summary statistics available in the literature for evaluating the forecast errors of any model, time series or econometric. We often do not compute all the statistics mainly because one of them is the function of the other. Thus, here an attempt is made to identify the best models for garlic production in Bangladesh using the following contemporary model selection criteria, such as RMSPE, MPFE and TIC.
Root mean square error percentage (RMSPE): Root Mean Square Error Percentage (RMSPE) is defined as:
 |
where, Ytf is the forecast value in time t and Ytα is the actual value in time t.
Minimum phone frame error (MPFE): Minimum Phone Frame Error (MPFE) is defined as:
where, Yαt is the actual value in time t and Ytf is the forecast value in time t.
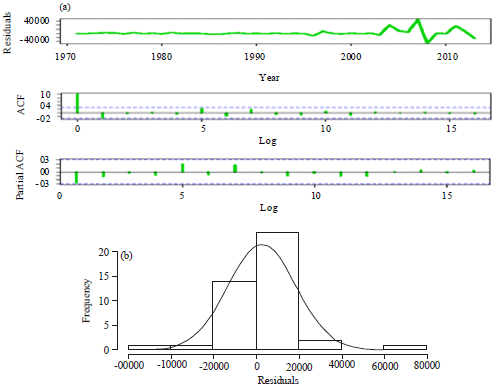
Theil inequality coefficient (TIC): Thail (1966) Inequality Coefficient (TIC) is defined as:
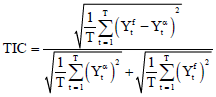 |
where, Ytf is the forecast value in time t and Ytα is the actual value in time t.
Most of the studies cited in this study identify the health benefit of garlic. They have shown that garlic is effective in reducing total cholesterol, helps eliminating waste materials and dangerous free radicals from the human body. Thus it is necessary to identify the amount needed for a country to make decision about import or export. The previous studies cited in this paper not consider the amount of production. However, in this study we are dealing with production and make forecast about future production of garlic. To forecast the future production a Time series model considered in this study. During the study period, the average garlic production in Bangladesh is around 67 thousand ton per annum with a standard deviation 56644.4576 ton. The maximum production was 233609 ton in the year 2012 and the minimum production was 29 thousand ton in the year 1996. In this study, Augmented-Dickey-Fuller (ADF) unit root test, Phillips-Perron (PP) unit root test and Kwiatkowski-Phillips-Schmidt-Shin (KPSS) unit root test are used to check, whether the data series is stationary or not. After second differencing the Augmented-Dickey-Fuller (ADF) test with Pr (|τ|≥-6.1937)<0.01 and Phillips-Perron (PP) test with Pr(|τ|≥-55.0558)<0.01 at 5% level of significance adequately declared that the data series is stationary and suggest that there is no unit root and also the Kwiatkowski-Phillips-Schmidt-Shin (KPSS) unit root test declared that the data series is stationary and suggest that there is no unit root with Pr(|τ|≥0.0429)<0.1 at 5% level of significance. The graphical representations of the original and second differenced series are presented in Fig. 1a and b.
It is clear that the garlic production data series shows initially almost equal production up to the year 2003 bur there is a dramatic increasing trend after the year 2003 may due to revolution in agricultural sector in Bangladesh, i.e., the variance is unstable which leads the garlic production data series is not stationary (Fig. 1a). However, it is clear that the second differenced garlic production data series shows stable variance, which leads the data becomes stationary. To stabilize the variance and to make the data stationary second difference is enough that is difference order is 2 and it is said that integrated of order 2 (Fig. 1b). The alternative positive and negative ACF (Fig. 1c) and exponentially decay PACF (Fig. 1d) indicates an autoregressive moving average process. Using the tentative procedure, it is clear that ARIMA (0, 2, 1) model with AIC = 917.55, AICc = 917.87 and BIC = 920.98 is the best selected model for forecasting the garlic production in Bangladesh. The estimates of the parameters of the fitted ARIMA (0, 2, 1) model are shown in Table 1. Also, the value of the most useful "forecasting criteria" of the fitted ARIMA (0, 2, 1) model are shown in Table 1.
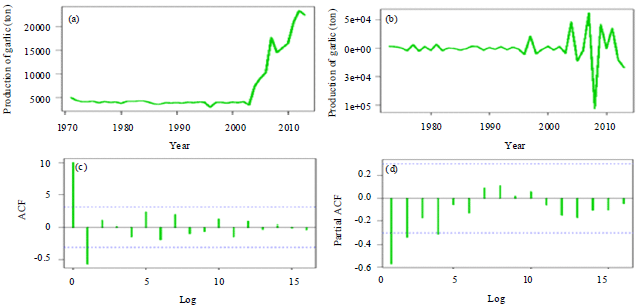
Several graphical test of the residuals for the fitted ARIMA (0, 2, 1) model are presented in Fig. 2, suggest that there is no significant pattern and hence there is no auto-correlation among the residuals.
 | |
| Fig. 1(a-d): | (a) Time series (original series) plot, (b) Time series (2nd differenced) plot, (c) ACF and (d) PACF of 2nd differenced garlic production in Bangladesh |
| Table 1: | Summary statistics and forecasting criteria of the fitted ARIMA (0, 2, 1) model |
 | |
Also, the "Box-Pierce" test with Pr(|χ12|≥1.5977) = 0.2062 and the "Box-Ljung" test with Pr(|χ12|≥1.7146) = 0.1904 at 5% level of significance strongly suggest to accept that there is no autocorrelation among the residuals of the fitted ARIMA (0, 2, 1) model. Here "Histogram with normal curve" is used to check the normality assumption of the residuals of the fitted model. The histogram with normal curve of the residuals of the fitted ARIMA (0, 2, 1) model is given in Fig. 2. Histogram with normal curve approximately, suggests that the residuals of the fitted ARIMA (0, 2, 1) model are normally distributed. Therefore, it is clear that our fitted ARIMA (0, 2, 1) model is the best fitted model and adequately used to forecast the garlic production in Bangladesh.
By using the best fitted model ARIMA (0, 2, 1), the forecasted garlic production and 95% confidence level for ten years are shown in Table 2.
The graphical comparison of the original series and the forecast series is shown in Fig. 3. It is apparent that the original series (dark-green-color) gradually shows an upward tendency. The forecast series (blue-color) fluctuated from the original series with a very small amount that is it shows the production in same manner of the original series (Fig. 3). Therefore, the forecasted series is really better representation of the original garlic production series in Bangladesh.
 | |
| Fig. 2(a-b): | (a) Several plots of residual plots and (b) Histogram with normal curve |
 | |
| Fig. 3: | Comparison between the original and forecasted garlic production in Bangladesh |
| Table 2: | Forecasted garlic production in Bangladesh |
 | |
| LCL: Lower confidence limit, UCL: Upper confidence limit | |
A time series model is used to identify the patterns in the past movement of a variable and uses that information to forecast the future values. This study tried to fit the best model to forecast the garlic production in Bangladesh with the help of the latest available model selection criteria, such as AIC, AICc and BIC, etc. The best selected Box-Jenkins ARIMA model for forecasting the garlic productions in Bangladesh is ARIMA (0, 2, 1). From the comparison between the original series and forecasted series shows the same manner indicating fitted model are statistically well behaved to forecast garlic productions in Bangladesh i.e., the models forecast well during and beyond the estimation period, which reached at a satisfactory level. Thus, this model can be used for policy purposes as far as forecasts the garlic production in Bangladesh.