Research Article
Big Bang Algorithm: A New Meta-heuristic Approach for Solving Optimization Problems
Department of Mathematics, University of Raparin, Ranya, Kurdistan Region, Iraq
LiveDNA: 98.15322
Big Bang Algorithm (BBA) is related to two principle concepts. In general, BBA ties to artificial agent or artificial particles clearly and to, natural event in the universe; big bang, extension of galaxies, rotation of planets and getting away of galaxies from each other. It comes from both evolutionary programming and genetic algorithms. In this paper, relationships between BBA and above concepts are obvious.
Recently, so many different heuristic and meta-heuristic approaches have been proposed by optimization scientists1-11. Almost all of these algorithms are based on behavior of animals and life natural systems. The most famous meta-heuristic algorithms as follows: Ant Colony Optimization (ACO)3, Particle Swarm Optimization (PSO)4, Artificial Bee Colony Algorithm5, krill herd algorithm6, Bat Algorithm (BA)7, social spider optimization8, Chicken Swarm Optimization (CSO)9, firefly algorithm10 and laying chicken algorithm11.
This study introduces a new optimizer to optimize constraint and non-constraint programming problems in different continuous states. The algorithm discovered in simulating of a natural event model. The author introduces the big bang algorithm concept and discusses the steps of its extension from natural simulation system to optimizer. It is easy to show that the proposed simulated algorithm is successful using presented numerical results of linear and non-linear test problems.
The proposed big bang algorithm by the author comes from an easy natural theory of the creation of the universe such that the performance of steps will be displayed in a few lines of MATLAB code. It only requires storing feasible solutions and essential mathematical factors in two arrays. Therefore the algorithm has a great computational complexity in both of time and memory. In initial testes, the author has realized the enforcement to be effective and feasible by solving different kinds of problems. As mention, BBA discovered in simulating of a natural event model unlike all of previous meta-heuristic approaches2-11 which based on behavior of animals or insects. In the rest of paper, simulation of the algorithm from the big bang theory is introduced in details. Performances of steps and their MATLAB code will be presented. Finally use of approach for solving several class of problems, such as constraint and unconstraint programming problems in different states, is discussed.
SIMULATION OF BIG BANG THEORY
An estimated 13.7 billion years ago a particle popped which was an infinitely small, infinitely hot, infinitely dense something12. This is a great idea to create a very dense initial feasible solution in the feasible region. Here dense solution is a collection of solutions that are very near to each other. In this paper all solutions are centralized as an initial solution same as the initial particle in the universe.
The infinitely dense something explosively inflamed in space12. This is a great idea to create the first population of solutions. In fact the solutions, which were very near to each other, will be distributed in the feasible space same as the big bang phenomenon.
The universe continues to expand. Galaxies continue to rotate and move away from each other12. This phenomenon is the next concept which will be simulated by rotation of the best solution. In fact the best solution rotates around initial solution as a center point to find optimal solution.
In general, this paper focuses on creation of the universe simulation and answer of this question: "how was created this universe?" In this paper, solutions are created same as planets and galaxies by something like explosion. In fact, each galaxy or planet in the universe displays a feasible solution in continuous programming problem and they search to the optimal solution by turning around the initial solution.
Pheromone of ants in ant colony, individual members or global best in particle swarm optimization, crossover or combination of genes in genetic, are the fundamental concepts of some of the meta-heuristic algorithms. Here dear God created this universe using explosion; this concept is base to development of the proposed big bang algorithm.
BIG BANG ALGORITHM CONCEPT
The big bang algorithm optimizer will have the best presentation by its conception development description. As mentioned, BBA comes from the big bang theory, an original naturel event, so in this section the principle concepts of BBA and its relationship with the inspiring event are discussed.
Initial solution and population: The simulated algorithm already has been prepared based on two main concepts: initial solution and population. Same as the first small particle in the universe, the dense initial feasible solution is required in the feasible space. In this stage, the first population of solutions is generated very near to the initial feasible solution as a very dense initial solution. In fact, each solution in the initial population is created in the following neighborhood of initial solution in Rn:
| (1) |
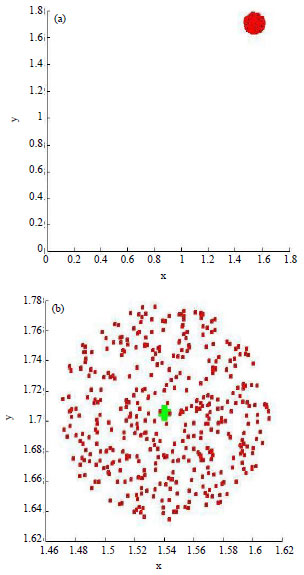 | |
| Fig. 1(a-b): | Four hundred solutions have been created near to initial solution (green point) |
![]()
ε is a very small positive real number and x0 is the initial solution.
This population is generated randomly in the possible nearest neighborhood of in x0 Fig. 1, 400 galaxies (feasible solutions) near to the initial solution has been shown for a given problem with = 0.005 in Rn Fig. 1a shows initial solution and the first population as a very dense and small particle and Fig. 1(b) shows them in the larger size.
As mention, initial solution and the first population have been created randomly. So if the created initial solution is not feasible, a loop in the MATLAB code is repeated to generate a feasible one. The pseudo code of that is proposed in Table 1.
| Table 1: | Pseudo code of initial solution and the first population |
 | |
Improving of population: Each solution of population will be moved from initial solution to the space after the big bang simulation. In fact, they would be changed in direction the vector which connects the initial solution and that solution. All solutions have been modified as follows:
| (2) |
d0j, is the vector from x0 to xj, 0<d0j < ε and:
| (3) |
States of α will be proposed as follows:
If →0 using (2) xj+1→xj even if then then α<1 then:
| (4) |
So, xj+1 will be little changed therefore interval 0<α< will not be selected and even if ![]() , nεN then:
, nεN then:
| (5) |
This state is not suitable for very large and very small n, because by large number the solution will not be changed and by small number the algorithm will miss very solution near to the initial solution. Also the changes should not be small because of the main feature of the big bang theory, so we let ![]() using (2) again and d0j = ε we have:
using (2) again and d0j = ε we have:
| (6) |
Which, k∈N. By solving test problem the author found n = 10 is a suitable choosing. Therefore the interval for as follows:
| (7) |
If α>> M, M is sufficiently large positive number, using (2):
| (8) |
Finally the author choices the best interval for as follows:
| (9) |
For every solution in the core of the small particle, initial solution here, one of these numbers k = {1, 2, 3, 4,.. } is selected and the solution is changed using (2) and (9).
Position of one solution which has been far from the initial solution after big bang is shown by Fig. 2a, 5 and 20 solutions, respectively with ε = 0.05, M = 1000, kε [1, 20], 2< α <40, k is a integer number as shown by Fig. 2b and c. Pseudo code of the stage is shown by Table 2.
By this stage, solutions are distributed in the feasible space. Already solutions were very near initial solution but here they have been improved. The best solution has been found and it will be prepared to search the optimal solution in a circle with initial solution as center in the next stage.
Rotation of the best solution: The last part of the simulation of the algorithm was inspired from rotation of the planets or galaxies. In this stage the best solution will be rotated on a circle with initial solution as a center point to find a better solution. This is because direction of the gradient vector for any objective function is defined as one of direction in 360°. But finding the better solution on a circle is a non-linear problem and it is not simple. So some points on the circle have been selected by randomly again. By this policy the author wants to reduce the complexity of the algorithm and to improve efficiency of the algorithm.
| Table 2: | Pseudo code of improving of population |
 | |
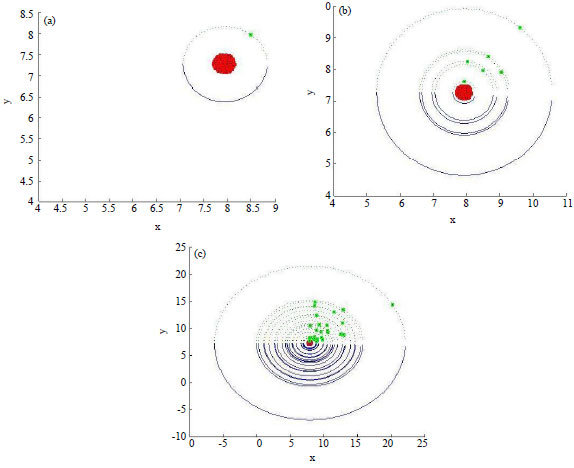 | |
| Fig. 2(a-c): | Process of improving of population |
 | |
| Fig. 3: | Searching for the better solution |
Red point in Fig. 3a shows the best solution from pervious stage. Its rotation to find a better solution has been shown in the Fig. 3b, the black point is the better solution after this process.
Improving solutions: The big bang algorithm searches for solution in a large space because of the main feature of the big bang theory. In fact, initial particle distributed in the very large space according to this theory. The author found BBA is missed solutions which are very near to the optimal solution in the constrained and small problems. So to solve these problems, some solutions will not be distributed and they should stay near the best solution at every iteration. By these solutions, BBA has more choices to find optimal solution. Efficiency of this stage has been shown using comparison results by this stage and without that in Example 2.
Steps of the algorithm and convergence: The principle steps of the big bang algorithm in will be Rn proposed as follows:
| • | The initial feasible solution (x01, x02, … , x0n), is created randomly. Number of solutions, N, two arbitrary small positive numbers ε1, ε and number of iterations, M1, are given and k = 1 |
| • | Initial population with N solutions is generated very near to (x01, x02, … , x0n) |
| • | Each solution j in step 2 will be changed in direction the vector that connects (x01, x02, … , x0n) to that solution by |
| • | The best solution searches to the better solution by rotation on the circle with initial solution as center. The best solution has been changed to the better solution if there is any better solution |
| • | Let (x01, x02, … , x0n) = (xbest1, xbest2, … , xbestn). If k>1 go to the next step otherwise let k = k+1 and go back to step 2 |
| • | If |
![]()
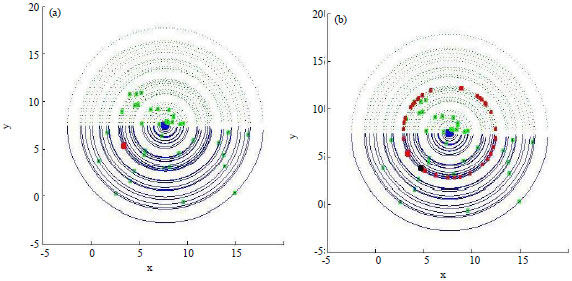
Figure 4 shows the process of the algorithm to find optimal solution from an initial feasible solution. Description of Fig. 4 has been proposed in the following paragraph.
A very dense initial solution, which includes initial population, is generated in (1), Red point is the initial solution and the blue point is the optimal solution. Population of solutions (green points) has been shown in (2) After step 3. In (3) Red points show the movement of the best solution in the current population to find a better solution. The better solution has been shown in (4) (large red point) this is the end of iteration 1. Next population will be created very near to the best solution from previous population and distributed in the space according to the (5). BBA has found the optimal solution in (6).
Following theorems show that the proposed algorithms are convergent.
Theorem 1: Every Cauchy sequence in real line and complex plan is convergent.
Proof: Proof of this theorem is given by Silverman13.
 | |
| Fig. 4(a-f): | Process of improving of population, (a) Step1: Initial solution and population, (b) Step 2: Improving population, (c) Step 3: Rotation of the best solution, (d) Step 4: Improving of the best solution (e) Step 5: New population and (f) Step 6: Optimal solution |
Theorem 2: Sequence {Fk} which was proposed in the proposed algorithms are convergent to the optimal solution, so that the algorithms are convergent.
Proof: Proof of this theorem is given by Hosseini14.
Relationship between big-bang theory and BBA: In the big bang theory, the universe is started by a very small and dense particle. Like this first small particle in the universe, a small and dense initial feasible solution has been simulated which starts BBA. In this simulation a set of feasible solution, as the first population, are generated very near to each other. Mathematical form of this simulation has been shown in (1) in which ε is a very small positive real number and shows that solutions are near each other (Fig. 1).
In the next stage of the big bang theory, infinitely small and dense particle is exploded in the space. Similarly, in the proposed simulated algorithm, solutions which were too near each other are distributed in the feasible space of the optimization problem. In the second step of the BBA every solution of the first population is moved from initial solution, as a center of population. Formulation of this concept has been shown in equation (2) which shows the movement of solutions in a defined direction.
The last concept of the big bang theory is the expansion of the universe and rotation of galaxies and move away from each other. Same as this phenomenon in the next step of the algorithm, the best solution of the population is rotated around initial solution to find a better solution and all solutions will be distributed in the space again and moved away from the best solution as the center.
COMPUTATIONAL RESULTS AND DISCUSSION
Example 1
Consider the following four peak function problem:
![]()
Which (x, y) ε [-5, 5]Χ[-5 5].
This problem has two local peaks with and two global peaks with f = 1 at (4, 4) and (-4, 4) and two global peaks with f = 2 at (0, 0) and (0, -4).
For solving the problem by BBA, all efficient factors are: number of solutions (galaxies), small positive number ε, initial feasible solution, M = 1000 and α. According to the Table 3, the proposed meta-heuristic approach has obtained a solution with less time than firefly algorithm. Behavior of agents to obtain optimal solution has been shown in Fig. 5.
In Fig. 5, red points are local and global peaks, BBA obtains local peak in just one iteration according to Fig. 5a. Figure 5b s hows getting global peak in two iterations.
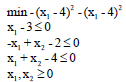
Example 2: Consider the following linear programming problem:
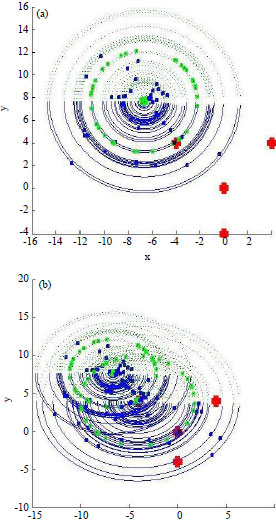 | |
| Fig. 5(a-b): | Big bang algorithm to find local and global peaks -Example 1 |
| Table 3: | Comparison of BBA and firefly algorithm to find global peak-Example 1 |
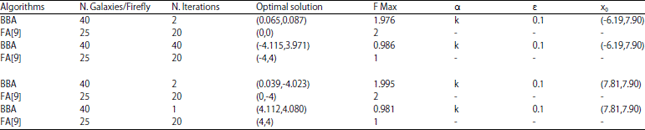 | |
| Table 4: | Comparison of BBA and other algorithms-Example 2 |
 | |
| Table 5: | Comparison of BBA and other methods- Example 3 |
 | |
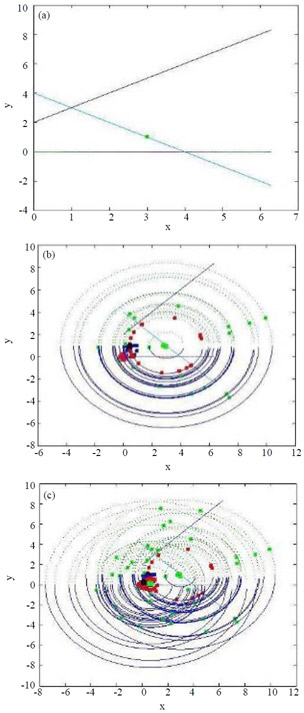 | |
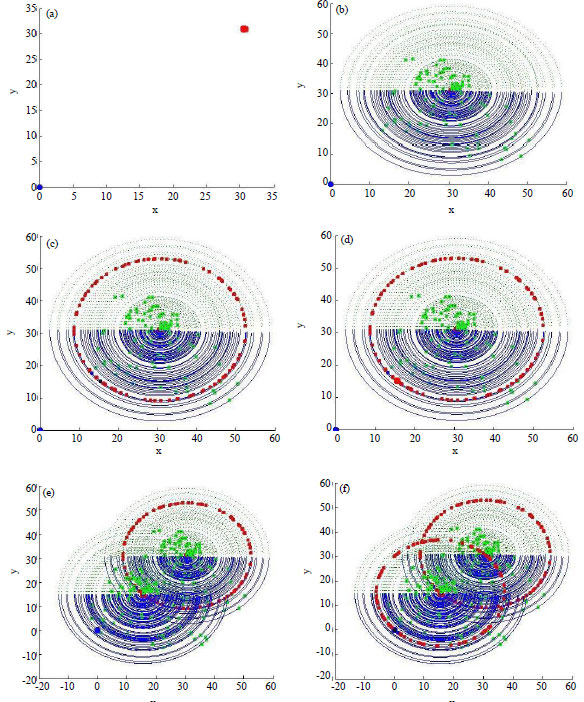
| Fig. 6(a-c): | Algorithm to find optimal solution-Example 2, (a) Initial Solution and feasible region, (b) First Iteration and (c) Second Iteration |
The above problem is a constrained problem, so some of solutions have to stay near to initial solution as mentioned before. In fact the problem has been solved by both of two states of the algorithm; the common steps and steps with hold on some solution near to the initial solution according to Table 4. The obtained solutions are better with the second strategy according to Table. M = 100 and other factors have been given in the Table.
Process of the algorithm to solve Example 2 is shown in Fig. 6. The proposed algorithm is efficient for problems by more than two variables according to the following example.
Example 3: Consider the following linear programming problem:
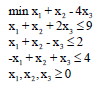
Comparison of LCA and exact methods has been proposed in Table 5. Behavior of generations to find optimal solution has been shown in Fig. 7.
Example 4: Consider the following linear bi-level programming problem:
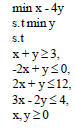
Using KKT conditions the problem will be converted to the following problem:
 | |
| Fig. 7(a-d): | Generations moves in the feasible region to find optimal solution-Example 3, (a) x0 and optimal solution, (b) Generation 1 after big bang, (c) Generation 2 and (d) Generation 3 |
| Table 6: | Comparison of BBA and other methods- Example 5 |
 | |
| Table 7: | Results of BBA for more test problems |
 | |
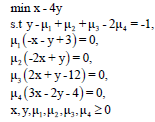
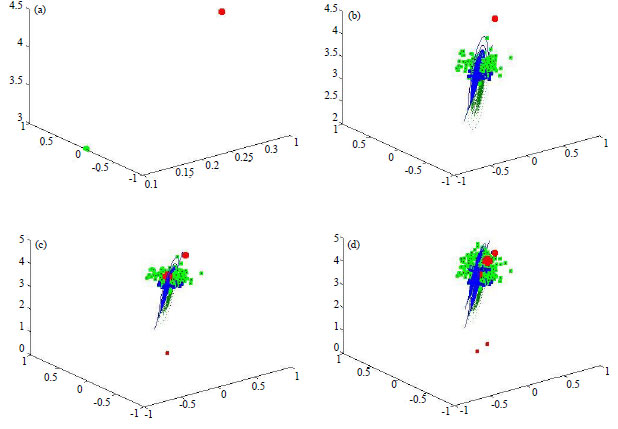
Comparison of BBA and other methods has been proposed in Table 6. Behavior of generations to find optimal solution has been shown in Fig. 8.
In Table 7 some benchmark has been solved by BBA. The big bang algorithm has been compared with classic method in Matlab based on simplex. In above Table Linprog is the function of this method in Matlab which searches for optimal solution by enumeration of vertex points of linear problem. So it has high computational complexity but BBA tries to get the optimal solution by random and population of solutions.
In comparison with laying chicken algorithm by Hosseini11 which is based on animal behavior, BBA is based on a scientific theory. In fact, most of meta-heuristic algorithms are based on animal’s behavior, such as krill herd: A new bio-inspiredoptimization algorithm by Gandomi and Alavi16 but BBA is the first meta-heuristic based on theories. A new algorithm has been proposed recently by Bazaraa et al.18 which is based on exact methods. The BBA is based on meta-heuristics which has simple Matlab code.
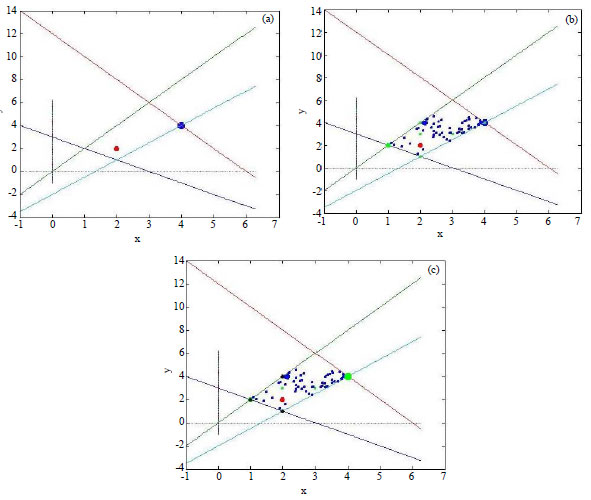 | |
| Fig. 8(a-c): | Process of finding optimal solution by BBA-Example 4, (a) Initial population, (b) Generation 2 and (c) Generation 4 and optimal solution for BLPP |
BBA was proposed as a natural event algorithm, not based on swarm intelligence or behavior of animals unlike almost all of pervious proposed meta-heuristic approaches. It is a simple meta-heuristic method which can optimize different levels of functions and optimization programming problems. BBA was successful because it distributes solutions in all feasible space randomly. Perhaps the easy implementation of the algorithm and consuming time to obtain optimal solution, will be interested by researchers in the latter researches.
This study proposes an algorithm to solve optimization programming problems which is efficient for solving several kinds of mathematical programming problems. An efficient and feasible method based on big bang theory is presented in this study. The new meta-heuristic proposed algorithm in this paper is based on a natural phenomenon which has simple Matlab code. This new meta-heuristic perhaps will help the researchers to solve other NP-Hard problems of optimization area.
The author would like to extend his thanks to the Faculty of Mathematics, University of Raparin. Special thanks also for Quality Assurance of the university which supported this study.