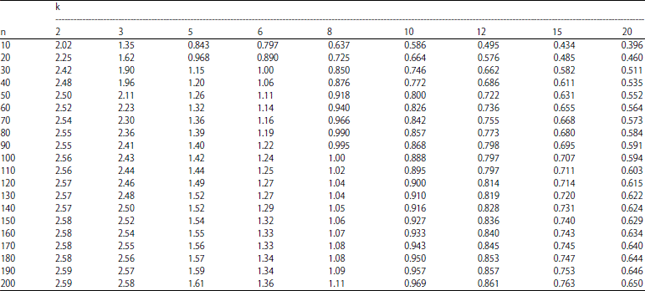
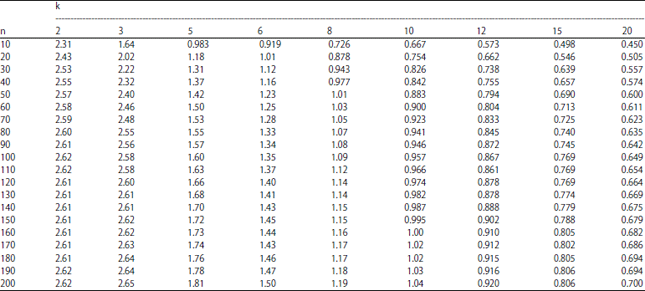
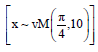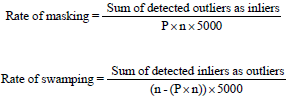Research Article
Robust Circular Distance and its Application in the Identification of Outliers in the Simple Circular Regression Model
Department of Mathematics, University Putra Malaysia, Jalan Upm, 43400 Serdang, Selangor,Malaysia
LiveDNA: 964.15431
Habshah Midi
Department of Mathematics, University Putra Malaysia, Jalan Upm, 43400 Serdang, Selangor,Malaysia
Sohel Rana
Department of Applied Science, East West University, Dhaka, Bangladesh
Abdul Ghapor Hussin
Faculty of Defence Science and Technology, National Defence University of Malaysia, Jalan Upm, 43400 Serdang, Selangor, Malaysia