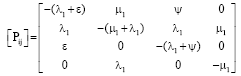Research Article
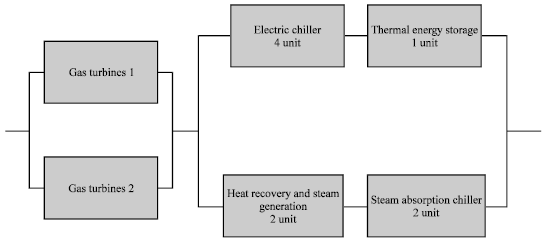
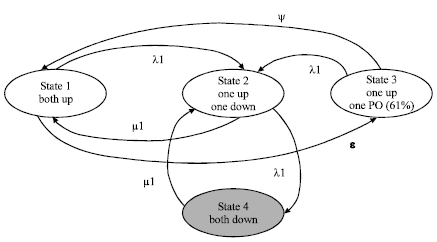
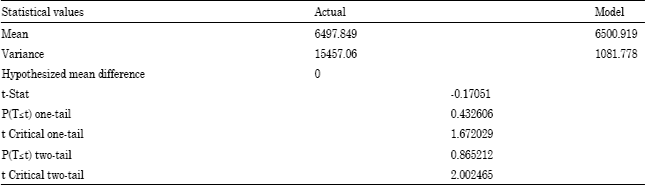
Multi-state System Availability Model of Electricity Generation for a Cogeneration District Cooling Plant
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Malaysia
Meseret Nasir
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Malaysia