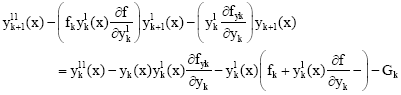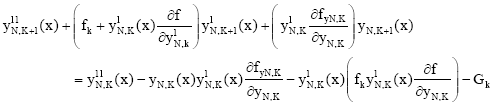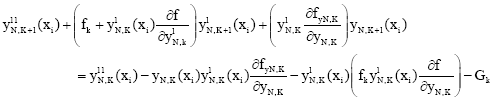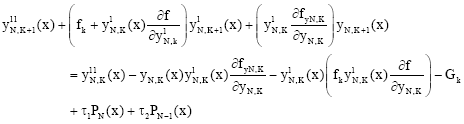Research Article
An Application Method for the Solution of Second Order Non Linear Ordinary Differential Equations by Chebyshev Polynomials
Department of Mathematics, University of Ilorin, Ilorin, Nigeria
LiveDNA: 234.24870
A. Abubakar
Department of Mathematics and Computer Science, Ibrahim Badamasi Babangida University, Lapai, Niger State, Nigeria