Research Article
Applying Genetic Algorithm to Fast and Precise Selection of GPS Satellites
Department of Electrical Engineering, Iran University of Science and Technology, Narmak, Tehran 16846-13114, Iran
The Geometric Dilution of Precision (GDOP) concept was originally used as a criterion for selecting the optimal 3D geometric configuration of satellites in GPS. When enough measurements are available, the optimal measurements selected with the minimum GDOP can help reduce the adverse geometry effects, thereby improving the location accuracy. However, excessive or redundant measurements may increase the computational overhead and may not provide significantly improved location accuracy. It is very critical to select a subset with the most appropriate measurement units rapidly before positioning (Chen and Su, 2010).
Several methods based on GDOP have been proposed to improve the GPS positioning accuracy (Zhu, 1992; Hsu, 1994; Phatak, 2001; Zhong and Huang, 2006; Zhang and Zhang, 2009). Most, if not all, of those methods need matrix inversion to calculate GDOP. Though they can guarantee to achieve the optimal subset, the computational complexity is usually too intensive to be practical.
The interest in Neural Networks (NNs) comes from the networks’ ability to mimic human brain as well as its ability to learn and respond. As a result, NNs have been used in a large number of applications and have proven to be effective in performing complex functions in a variety of fields. These include pattern recognition, classification, vision, control systems, approximation and prediction. Adaptation or learning is a major focus of neural net research that provides a degree of robustness to the NN model. In predictive modeling, the goal is to map a set of input patterns onto a set of output patterns. NN accomplishes this task by learning from a series of input-output data sets presented to the network. The trained network is then used to apply what it has learned to approximate or predict the corresponding output (Mosavi, 2007).
Instead of directly solving the GDOP equations and avoiding the complicated processing of matrix inversion, Simon and El-Sherief (1995) rephrase the GDOP calculation as approximation problems and employ NNs to solve such problems. However, solving classification and approximation problems using NN usually suffer from the long training time and difficulty in determining the NN architecture. Besides, the overfitting problem degrades the performance of NN applications when the numbers of features and training patterns are large. Though in the experimental results reported by Jwo and Chin (2002) and Jwo and Lai (2007), NN outperforms the traditional methods; the training time and performance can be further improved.
The Genetic Algorithm (GA) is a stochastic global search method that mimics the metaphor of natural biological evolution. GAs operate on a population of potential solutions applying the principle of survival of the fittest to produce (hopefully) better and better approximations to a solution. At each generation, a new set of approximations is created by the process of selecting individuals according to their level of fitness in the problem domain and breeding them together using operators borrowed from natural genetics. This process leads to the evolution of populations of individuals that are better suited to their environment than the individuals that they were created from, just as in natural adaptation (Kim and Adeli, 2001).
In this study, GA approach is applied for GPS GDOP approximation and classification, without complicated matrix inversion. GA is employed to learn the functional relationships between the entries of the GDOP measurement matrix and the final GDOP equations. This method is applicable to general GDOP calculation regardless to the number of satellite signals being processed by the receiver. The performance and computational benefits of using GA for GDOP approximation and classification are discussed.
GDOP CALCULATION USING CONVENTIONAL MATRIX INVERSION METHOD
In GPS applications the GDOP is often used to select a subset of satellites from all visible ones. In order to determine the position of a receiver, pseudo-ranges from n≥4 satellites must be used at the same time. By linearizing the pseudo-range equation with Taylor’s series expansion at the approximate (or nominal) receiver position, the relationship between pseudo-range difference (Δρi) and positioning difference (Δxi) can be summarized as follows (Doong, 2009):
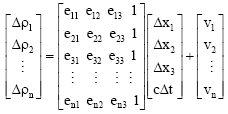 | (1) |
which is written in a compact form as:
| (2) |
The n≥4 matrix H is formed with direction cosines ei1, ei2 and ei3 from the receiver to the i-th satellite and V denotes a random noise with an expected value of 0. The difference between the estimated and true receiver positions is given by:
| (3) |
where, HT denotes the transpose of H and M = HTH, called the measurement matrix, is a 4x4 matrix no matter how large n is. It can be shown that the measurement matrix is symmetric and non-negative and thus it has four non-negative eigenvalues. Assuming E{VTV} = σ2I, then:
The GDOP factor is defined as the square root of the trace of the inverse measurement matrix:
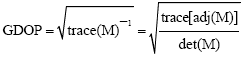 | (4) |
Because GDOP provides a simple interpretation of how much positioning precision can be diluted by a unit of measurement error, it is desirable to choose the combination of satellites in a satellite constellation with GDOP as small as possible.
STANDARD GENETIC ALGORITHM
GA starts with an initial population whose elements are called chromosomes. The chromosome consists of a fixed number of variables which are called genes. In order to evaluates and rank chromosomes in a population, a fitness function based on the objective function should be defined. Three operators must be specified to construct the complete structure of the GA procedure; selection, crossover and mutation operators. The selection operator cares with selecting an intermediate population from the current one in order to be used by the other operators; crossover and mutation. In this selection process, chromosomes with higher fitness function values have a greater chance to be chosen than those with lower fitness function values. Pairs of parents in the intermediate population of the current generation are probabilistically chosen to be mated in order to reproduce the offspring. In order to increase the variability structure, the mutation operator is applied to alter one or more genes of a probabilistically chosen chromosome. Finally, another type of selection mechanism is applied to copy the survival members from the current generation to the next one. Steps of GA implementations are as follows:
| • | Step 1: Initialization: Generate an initial population P0. Set the crossover and mutation probabilities pc∈(0,1) and pm∈(0,1), respectively. Set the generation counter t =1 |
| • | Step 2: Selection: Evaluate the fitness function F at all chromosomes in Pt. Select an intermediate population Pt' from the current population Pt |
| • | Step 3: Crossover: Associate a random number from (0, 1) with each chromosome in Pt' and add this chromosome to the parents pool set SPt if the associated number is less than pc. Repeat the following steps until all parents in SPt are mated |
| • | Choose two parents p1 and p2 from SPt. Mate p1 and p2 to reproduce children c1 and c2 |
| • | Update the children pool set Sct through SCt:= SCt ∪ {c1, c2} and update SPt through SPt:= SPt-{p1, p2} |
| • | Step 4: Mutation: Associate a random number from (0,1) with each gene in each chromosome in Pt', mutate this gene if the associated number is less than pm and add the mutated chromosome only to the children pool set SCt |
| • | Step 5: Stopping conditions If stopping conditions are satisfied, then terminate. Otherwise, select the next generation Pt+1 from Pt∪SCt. Set SCt to be empty, set t:= t+1 and go to step 2 |
GPS GDOP approximation using GA: In Eq. 4, GDOP is mainly evaluated by (HTH)-1, where geometry matrix H is given by Parkinson and Spilker (1996):
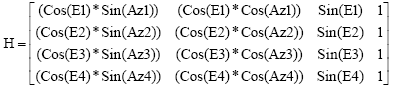 | (5) |
where, Ei and Azi are elevation and azimuth angles of satellite views in space with respect to receiver position, respectively. Nevertheless, it is not a good practice to invert the normal equations matrix (Su and Wu, 2008; Wu and Su, 2009). Since, M is a symmetric matrix, so it can be represented by Eq. 6:
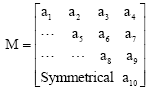 | (6) |
This study proposes GDOP approximation by linear combination of ai as Eq. 7:
| (7) |
The fitness function is the sum of squared error and is defined as:
| (8) |
where e = d-y, d is the target output and
is the output of method. Obviously the objective is to minimize J subject to weights wi. The wi coefficients are calculated by using GA.
GPS GDOP classification using GA: Suppose there are some 2-D data as are shown in Fig. 1. For classifying them, we can specify two lines F1(x,y) = a and F2(x,y) = b that make 3 areas as follows:
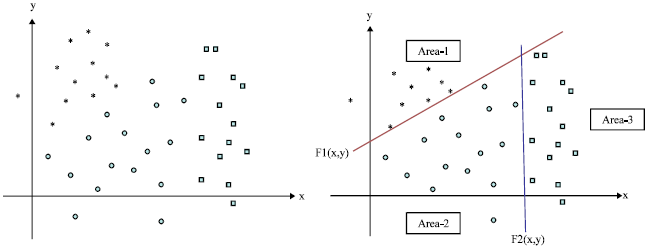 | |
| Fig. 1: | 2-D data classification (the legends of (*), (ο) and (□) present three types data) |
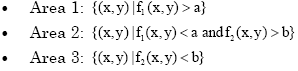 |
In the search space, every constellation of four GPS satellites is represented as a seven dimensional element containing arrays of matrix that use for the GDOP calculation:
GA by using these characteristics provides two linear vectors that classify GDOP into 3 groups.
| (9) |
| (10) |
where, F1 and F2 are two thresholds for GDOP classification. The wi coefficients are calculated by using GA. Similarly, classification into more groups is feasible based on the same philosophy.
COMPUTER SIMULATIONS
The data file containing of 900 patterns was used for testing the proposed method. In Fig. 2a and b, the GDOP solutions by matrix inversion (using Eq. 4) is represented with -, the while the GDOP approximated by the proposed methods is shown by *. The GDOP residual is defined as the difference between the GDOP value by matrix inversion and by the proposed approach:
GDOPMatrix inversion-GDOPApproximated |
The maximum, minimum and Root-Mean-Square (RMS) error are used as the error measure for evaluating approximation performance. RMS value is computed using:
| (11) |
where, M is number of tests, GDOPMatrix inversion is the GDOP from direct matrix inversion obtained from Eq. 4 and GDOPApproximated is output of the model.
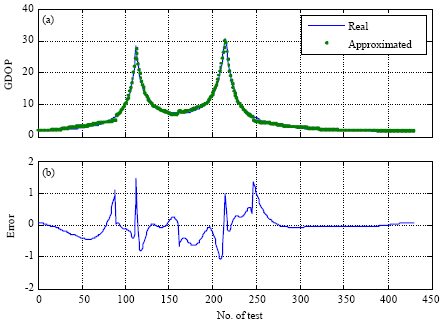 | |
| Fig. 2: | (a) Real versus approximated GPS GDOP and (b) its approximation error |
| Table 1: | Error of GPS GDOP approximation using the proposed method |
 | |
| Table 2: | Comparison of accuracy and CPU time of GA and NN approaches for GPS GDOP calculation |
 | |
| Table 3: | GDOP classification |
 | |
Table 1 shows three statistical measures of approximations error using the proposed method.
Table 2 presents the comparison of accuracy and CPU time of GA and NN approaches for GPS GDOP calculation. The simulation results demonstrate that GA approach is accurate and faster than NN approach.
The data file containing of 900 patterns was used for testing the proposed classification method. For data classification according Table 3, G1 = 3 and G2 = 5 are considered.
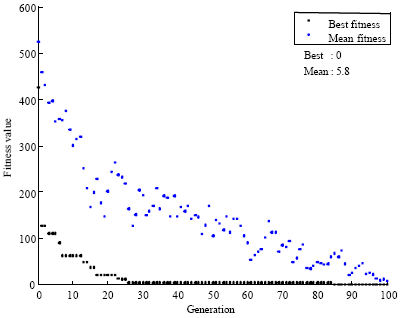 | |
| Fig. 3: | The value of fitness function for GPS GDOP classification (GDOP<3 and GDOP>3) |
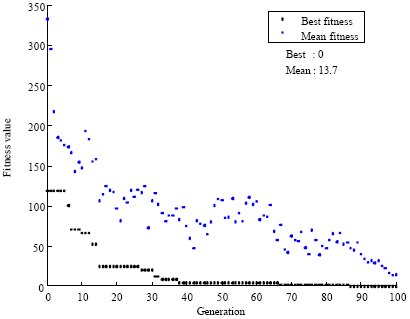 | |
| Fig. 4: | The value of fitness function for GPS GDOP classification (3<GDOP<5 and GDOP>5) |
At first, all data were divided into two categories. Class1 that their GDOP values are smaller or equal to 3. Class 2 that their GDOP values are lager than 3. Then, the data with GDOP>3 were divided into two categories. First class that their GDOP values are smaller or equal to 5. Second class that their GDOP values are lager than 5.
Figure 3 and 4 show the value of fitness function that expresses the number of errors in classification. As you can see GA classify these data with 100% accuracy. This experiment was performed with G1 = 3 and G2 = 6 and similar results were obtained.
Simon and El-Sherief (1995), Jwo and Chin (2002) and Jwo and Lai (2007) approximate and classify GPS GDOP using NNs. Advantages of the proposed method based on GA in this study than references of mentioned are simple, low cost, easy to design and accurate. It has the structure complexity less than for hardware implementation. It also requires the memory less than for software implementation.
To analyze the performance of navigation it is necessary to calculate the DOP that provides positioning accuracy. Among number visible satellites from the user’s position, a set of satellites which are in better geometry is needed to find minimum GDOP. The matrix inversion method for GDOP calculation is rather time consuming and presents a calculation burden. This paper has presented application of GA for GPS GDOP precise modeling without complicated matrix inversion. GAs are computer programs that mimic the processes of biological evolution in order to solve problems and to model evolutionary systems. Using the proposed method, the calculations costs of GPS GDOP can be reduced. In compare with neural network approach, GA is faster and more precise for approximation and classifying GPS GDOP. So with the proposed method, the processing costs for GPS positioning with low GDOP can be reduced (no need to training time and powerful processor). The results show that the proposed method has high degree of accuracy and the number of training iterations is greatly reduced.