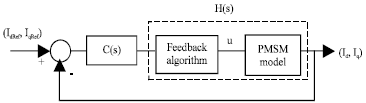
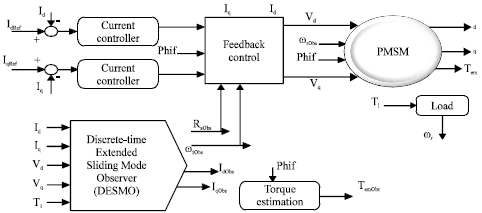
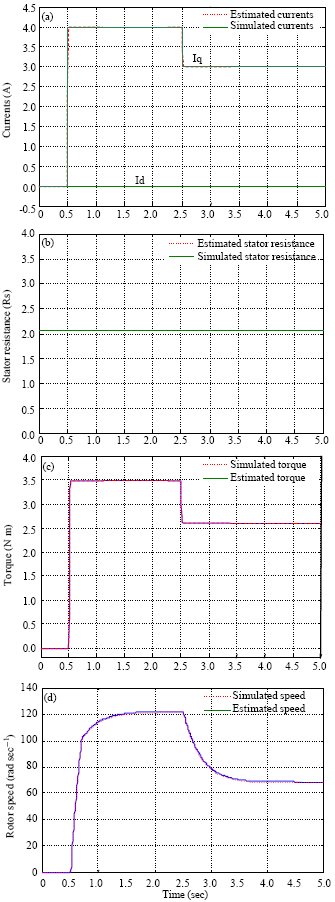
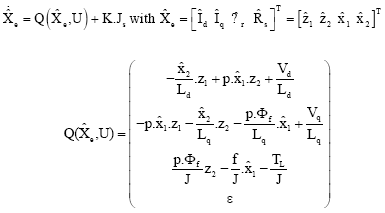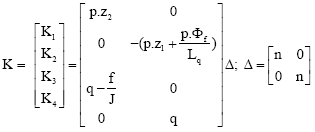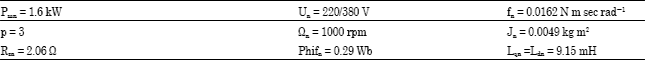Review Article
Nonlinear Feedback Linearization and Observation Algorithm for Control of a Permanent Magnet Synchronous Machine
Department of Electrical and Electronic Engineering, Institut National Polythechnique Houphouet Boigny (INPHB) BP 1093 Yamoussoukro, C�te d�Ivoire, France
T.R. Ori
Department of Electrical and Electronic Engineering, Institut National Polythechnique Houphouet Boigny (INPHB) BP 1093 Yamoussoukro, C�te d�Ivoire, France
K.E. Ali
Department of Electrical and Electronic Engineering, Institut National Polythechnique Houphouet Boigny (INPHB) BP 1093 Yamoussoukro, C�te d�Ivoire, France
Z. Yeo
Department of Electrical and Electronic Engineering, Institut National Polythechnique Houphouet Boigny (INPHB) BP 1093 Yamoussoukro, C�te d�Ivoire, France
S. Ouattara
Department of Electrical and Electronic Engineering, Institut National Polythechnique Houphouet Boigny (INPHB) BP 1093 Yamoussoukro, C�te d�Ivoire, France
X. Lin-Shi
Universite de Lyon, AMPERE, INSA Lyon, CNRS UMR 5005, Villeurbanne 69621, France