Research Article
Analysis of Capacitance Networks
Department of Physics, College of Sciences, University of Tabuk, P.O. Box 1144, Dhiba Road, Tabuk, Kingdom of Saudi Arabia
INTRODUCTION
Infinite resistive network problems have served as excellent vehicles for helping physics students and electrical engineering recognize and appreciate the power and superposition and symmetry in the analysis of electrical networks. These problems have been studied and illustrated well using random walk approach (Jeng, 2000), superposition and symmetry approach (Venezian, 1994; Atkinson and Steenwijk, 1999; Asad et al., 2005c) and finally using the so-called Lattice Green’s Function approach (Cserti, 2000; Asad et al., 2004, 2005a, b, c, 2006) . A special case of this class of problems involves the calculation of the effective resistance between two adjacent nodes of an infinite uniform two-dimensional (2D) resistive lattice.
In particular, the effective resistance between two adjacent nodes of the 2D Liebman resistive mesh (i.e., infinite 2D square resistive lattice) was calculated by Aitchison (1964) and the result was found to be (1/2)R. Bartis (1967) calculated the resistance between adjacent nodes for three other infinite 2D resistive lattices, the triangular, Honeycomb and kagome lattices. He found that the effective resistances to be (1/3)R, (2/3)R and (1/2)R, respectively. Aitchison (1964) and Bartis (1967) showed how to analyze infinite 2D resistive networks using the undergraduate level (i.e., Ohm’s and Kirchhoff’s Laws).
Now is it possible to analyze complex infinite networks using undergraduate principles and laws?
This note is written to answer the above question. So, the aim of this note is to show that infinite 2D networks consisting of identical capacitors each of capacitance 1-farad can also be treated and given to the undergraduate level. The method used in this short note is the same as that presented in Bartis (1967). So, here we introduce the problem with its complete solution as a counter example.
The problem here is the determination of the equivalent capacitance between adjacent nodes of a square infinite network consisting of identical capacitors each of 1-farad capacitance. To do this, let us concentrate at a given element C near the center of Fig. 1 and assume the charge passing through in two cases: First, consider a potential difference of m- Volt exists between one end of C and the other four sides of the network at infinity; Second, consider a potential difference of m- Volt is established between infinity and the other end of C.
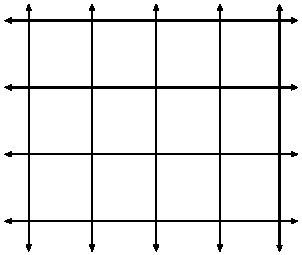 | |
| Fig. 1: | Infinite square network consisting of identical capacitors each of capacitance 1-farad |
 | |
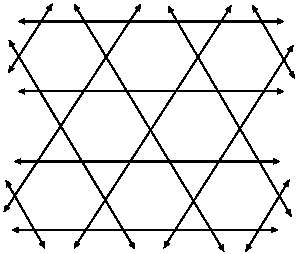
| Fig. 2: | Infinite triangular network consisting of identical capacitors each of capacitance 1-farad |
It is clear from the symmetry of the situation that in both cases listed above a quarter of the charge passes through C. Now superimpose these two cases, choosing m such that the potential difference across C is 2-Volt. Thus it is easy to see that half of the charge then flows through C. From Ohm’s law, the charge in C is 2-coulomb. Therefore, it follows that the total charge flowing in the network is 4-coulomb and as a result its effective capacitance between adjacent nodes is 2-farad. The same result was recently obtained by Asad et al. (2004) using LGF method and Asad et al. (2006) using the superposition of charge distribution method.
The above analysis can also be applied to other networks (i.e., triangular, honeycomb and kagome networks) but with some minor changes (Fig. 2-4). Now, assuming all the elements of Fig. 2-4 have a capacitance of 1-farad, one can finds that the equivalent capacitance between adjacent nodes for the earlier mentioned networks is equal to 3-, 3/2- and 2- farad, respectively.
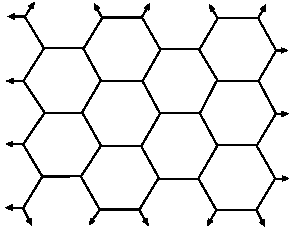 | |
| Fig. 3: | Infinite honeycomb network consisting of identical capacitors each of capacitance 1-farad |
 | |
| Fig. 4: | Infinite honeycomb network consisting of identical capacitors each of capacitance 1-farad |
CONCLUSION
It is important to notice that the present approach used to analyze the Capacitance network used the concepts of symmetry and the superposition. These two ideas are certainly not beyond the undergraduates. So, we can analyze the capacitance network for the undergraduate students. Finally, the content of this short note is helpful for electric circuit design. In this study, infinite complex 2D networks of identical capacitors has been analyzed using basic undergraduate principles. The results obtained in this study are very similar to those results obtained using complex methods (i.e., LGF method and superposition of charge distribution method which is based on complex mathematics.