Research Article
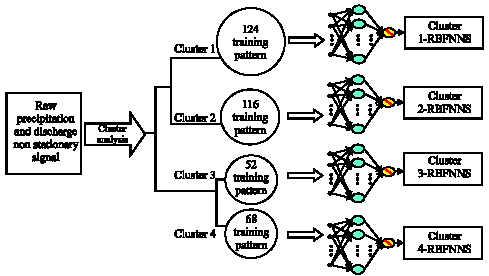
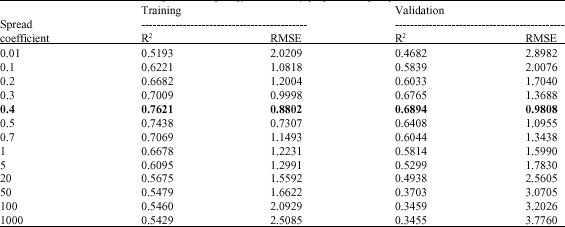
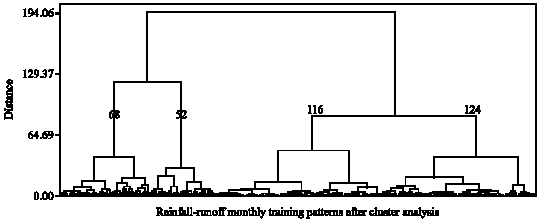
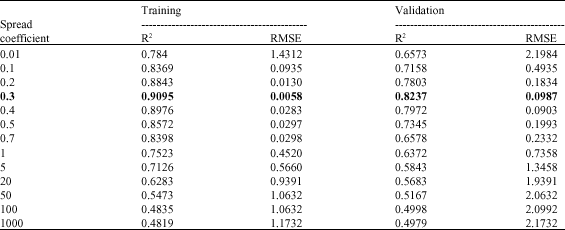
Cluster Analysis of Rainfall-Runoff Training Patterns to Flow Modeling Using Hybrid RBF Networks
Department of Watershed Management in Field of Water Resources,University of Tehran, Iran
M. Mahdavi
Faculty of Natural Resources, University of Tehran, Iran
A. Fakherifard
Faculty of Agriculture, University of Tabriz, Iran
A. Salajegheh
Faculty of Natural Resources, University of Tehran, Iran









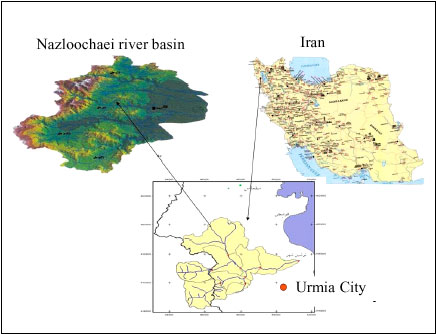
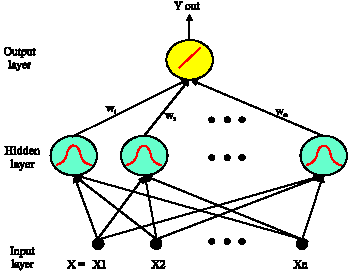
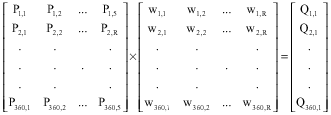
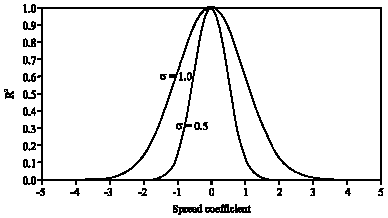
BLISSAG Bilal Reply
I search for THIS PAPER