Research Article
(-1, 1) and Generalized Kac-Moody Algebras
Jawaharlal Nehru Technological University, Anantapur Andhra Pradesh, India
LiveDNA: 91.11023
ORCID: 0000-0002-9765-7601
Associated with any algebra Θ over a field of char. ≠ 2 are two algebras denoted by Θ- and Θ+. There algebras have the same underlying vector space as Θ but are given the products [x, y] = x * y-y * x and x○y = ½(x * y+y * x), respectively, where * is the multiplication in Θ.
Albert (1948), proposed the problem of classifying all power-associative flexible Lie admissible algebras, whose commutator algebras are semi simple Lie algebras. Without assuming flexibility, Benkart (1984) classified all third power-associative Lie admissible algebras whose commutator algebras are semisimple Lie algebras. Myung (1985) classified all third power-associative Lie admissible algebras associated with the Virasoro algebra and the Witt albebra. Jeong et al. (1997) determined all third power-associative Lie admissible algebras whose commentator algebras are Kac-Moody algebras. In this study, we will determine all third power associative (-1, 1) algebras whose commutator algebras are simple generalized Kac-Moody algebras. Thedy (1975) collected information on two natural concepts in a right alternative algebra R, the submodule M generated by all alternators (x, x, y) and a new nucleus called alternative nucleus. He also studied the properties of (-1, 1) rings. Hentzel (1974), characterized the properties of (-1, 1) rings and showed that all simple (-1, 1) rings are associative. He developed several identities for (-1, 1) rings. Benkart (1982), classified all power-associative products * that can be defined on the algebra A of n/sup x/n matrices over a 2, 3-torsion free field F satisfying the condition x*y-y*x = xy-yx for all x, y ∈ A and stated that such product * are automatically Lie-admissible and they are Jordan-admissible too. Myung (1996) studied the properties of Lie-admissible algebras along with Virasoro algebra and determined third power associative Lie-admissible algebras whose commutator algebras are Virasoro algebras. Humphreys (1972), developed the basic general theory of Lie algebras to give a first insight into basics of the structure theory and representation theory of semisimple Lie algebras. It is noted that a 2, 3-torsion free right alternative algebra is a (-1, 1) algebra if it satisfies the identity (x, y, z) + (y, z, x) + (z, x, y) = 0.
Preliminaries: We begin with some of the basic facts about (-1, 1) algebras. Let (Θ, *) be a (nonassociative) algebra over the complex field ![]() with multiplication * and let (Θ‾, [,]) be its commutator algebra, where the underlying space is the same as Θ and the bracket operation [,]:Θ×Θ→Θ is defined by [x, y] = x * y-y * x for all x, y ∈ Θ.
with multiplication * and let (Θ‾, [,]) be its commutator algebra, where the underlying space is the same as Θ and the bracket operation [,]:Θ×Θ→Θ is defined by [x, y] = x * y-y * x for all x, y ∈ Θ.
An algebra Θ is called a (-1, 1) algebra if it satisfies the identity:
| (1) |
| (2) |
where, (x, y, z) = (xy)z - x(yz) denotes the associator of elements x, y and z. Identity (1) is meant to imply that Θ is right alternative and (2) implies that Θ is Lie-admissible, that is, the commutator algebra Θ‾ with a product [x, y] = xy - yx is a Lie algebra.
| (3) |
For a (-1, 1) ring (Θ, *), the multiplication * can be written as
| (4) |
Equation 3 is equivalent to
| (5) |
for all x ∈ R which can be linearized to
| (6) |
for all x, y ∈ R. Again linearizing (6) we obtain
| (7) |
for all x, y, z ∈R
The structure of generalized Kac-Moody algebras has been considered by many authors (Kac, 1990). A generalized Kac-Moody algebra is a Lie algebra that is similar to a Kac-Moody algebra, except that it is allowed to have imaginary simple roots.
Generalized Kac-Moody algebras are also sometimes called GKM algebras. The best known example is the monster Lie algebra. Most properties of GKM algebras are straight forward extensions of the usual properties of Kac-Moody algebras. A GKM algebra has an invariant symmetric bilinear form such that (ei, fi) = 1. There is a character formula for highest weight modules, similar to the Weyl-Kac character formula for Kac-Moody algebras except that it has correction terms for the imaginary simple roots.
A symmetrized Cartan matrix is a (Possibly infinite) square matrix with entries xij such that:
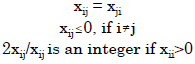 |
The universal generalized Kac-Moody algebra with given symmetrized cartan matrix is defined by generator ei, fi and hi and relations:
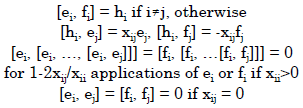 |
These differ from the relations of a (symmetrizable) Kac-Moody algebra mainly by allowing the diagonal entries of a Cartan matrix to the nonpositive. In other words we allow simple roots to be imaginary, whereas in a Kac-Moody algebra simple roots are always real.
A generalized Kac-Moody algebra is obtained from a universal one by changing the certain matrix by the operations of killing something in the center or taking a central extension or adding outer derivations.
We will use the identities (3), (4), (5), (6) and (7) frequently in determining the third power-associative (-1, 1) multiplications on generalized Kac-Moody algebras and our approach is based on the techniques developed by Benkart (1984), Jeong et al. (1997) and Myung (1996).
Let A = (aij)i, j∈I be a generalized Cartan matrix where I is the finite index and g = g (A) be the generalized Kac-Moody algebra associated with A. We will determine all the third power associative (-1, 1) structures on the generalized Kac-Moody algebra g = g (A). When A is of finite type, this problem was settled by Benkart (1984). Hence we will assume that the generalized Cartan matrix is not of finite type.
We start with two technical Lemmas, which support the rest of the results and the proof of these Lemmas can be found in (1997).
Main section
Lemma 1: The algebra of linear functional on K is an integral domain. In particular, if x ∈ Φ is a root of g and f: K →![]() is a linear functional on K satisfying f(h)x(hʹ) + f(hʹ)x(h) = 0 for all h, hʹ ∈ K then f = 0.
is a linear functional on K satisfying f(h)x(hʹ) + f(hʹ)x(h) = 0 for all h, hʹ ∈ K then f = 0.
Lemma 2: Let A = (aij)i, j ∈ I be a generalized cartan matrix which is not of finite type. If aij≠0 for some indices i, j ∈ I, there exists a root β = ΣxεI ck xk ∈ Φ of g such that ci>0, cj>0 and ci≠cj.
Remark: Lemma 2 holds for all generalized cartan matrices that are not of type An see (1972), (1990).
Let B be an abelian group, K be the vector space over F. Denote by FB the group algebra of B over F. The elements tc, c ∈ B from a basis of this algebra and the multiplication is defined by tctd = tc + d. We shall write 1 instead of t0. The tensor product M = FB ⊗F K is a free left FB- module. Denote an arbitrary element of K by d. For the sake of simplicity we write tcδ instead of cc⊗δ. We fix a pairing Φ: K× B → F which is F-linear in the first variable and additive in the second one. For convenience we use the following notations:
for arbitrary δ ∈ k and c ∈ R.
The following multiplications:
for arbitrary c, d ∈ R and δ1,δ2 ∈ K make g into a Lie algebra, called a generalized Kac-Moody algebra.
Let gc = tc k for x ∈ R, in particular go = K then [gc, gd] ⊂ gc+d holds for all c, d ∈ B. This means that g is a B-graded Lie algebra. It is clear that [δ, tcδ1] = δ(x)+tcδ1, hence δ is semisimple. Consequently K is a torus.
Let Bo = {x ∈ B/<δ, x> = 0, ∀ δ∈ K} and Ko = {δ ∈ K/<δ, x> = 0, ∀ δ ∈ B}. Φ is said nondegenerate if Bo = 0 and Ko = 0.
Lemma 3:
| (i) | The Cartan sub algebra K is closed under ο. |
| (ii) | For each x ∈ B/{0}, there exists a linear functional fx: K→C and a by linear map ux: K×K→K such that: |
| (8) |
for all δ ∈ K, txδx ∈ gx and the fx satisfies:
| (9) |
for all δ, δʹ ∈ K.
Proof:
| (i) | By bilinearity and commutativity of ο it suffices to show that δοδ ∈ K. write: |
It follows from [δ, δοδ] = 0 that
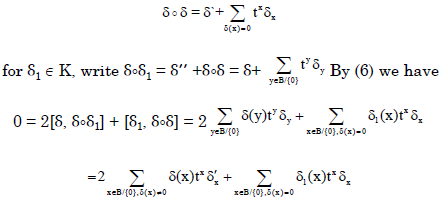 |
Hence, if δ(x) = 0, then δ1(x)txδx = 0 for all δ1 ∈ K which implies δx = 0. Therefore δοδ = δʹ ∈ T.
| (ii) | Write δοtxδx = δʹ + |
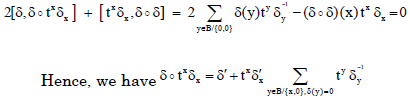 |
Similarly, for δ1 ∈ K, we have:
By (7), we have [δ, δ1οtxδx] + [δ1, txδx δ] + [txδx, δοδ1] = 0 which yields
| (10) |
By (10), one can easily find that
Denote δοtxδx = ux(δ, δx) + txδ(δ, δx) where ux(δ, δx) and δ(δ, δx) ∈ K. By:
We can find:
| (11) |
Fixing δʹ ∈ K so that δʹ(x) = 1, we see that if δ(x) = 0, δ(δ, δx) = (δοδʹ)(x)txδx and 2 δ(δʹ, δx) = (δʹοδʹ) (x)δx
Define ![]() for all δ ∈ Ker x: = {δ ∈ K/δ(x) = 0} and
for all δ ∈ Ker x: = {δ ∈ K/δ(x) = 0} and ![]() .
.
Since, K = Kerx ⊗ Fδʹ, fx is well defined. Then δοtxδx = fx(δ)txδx + ux(δ, δx) since, δ(δ, δx) = fx(δ)δx. It follows from (13) that (11) is true. It is clear that ux: K× K → K is a bilinear map.
From the following Lemma we can see that the linear functional fx are the same for all x ∈ B/{0}.
Lemma 4:
| (i) | For all x, y ∈ B/{0}, fx = fy. We denote it by f |
| (ii) | For all δ, δʹ ∈ K, δοδʹ = f(δʹ)δ + f(δ)δʹ |
Proof: If dim K = 1, then K = Fδ and for any x ∈ B/{0}, δ(x) ≠ 0 since, B0 = 0. Hence for δ1, δ2 ∈ K, we have δ1 = δ2 if δ1(x) = δ2(x) for some x ∈ B/{0}.
from (9), we have 2fx(δ)δ(x) = (δοδ)(x).
So ![]() this means that fx = fy for any y ∈ B/{0}.
this means that fx = fy for any y ∈ B/{0}.
Now we suppose that dim K>1. If Tx ≠ Ty, then K = Tx + Ty and there exists δ1, δ2 ∈ K such that δ1(x) = 1, δ1(y) = 0, δ2(x) = 0, δ2(y) = 1 and K = Fδ1 ⊗ Fδ2(y) ⊗ (Tx Ç Ty). Let δ3 ∈ Tx ∩ Ty. For any δ, δʹ ∈ K, it follows from (9) that
| (12) |
In (12), let δ = δʹ = δ1 we have fx+y(δ1) = fx(δ1)
Let δ = δ1, δʹ = δ3 we have fx+y(δ3) = fx(δ3).
Similarly, we have fx+y(δ2) = fy(δ2), fx+y(δ3) = fy(δ3)
Let δ = δ1, δʹ = δ2, we have:
| (13) |
Now let z = 2x+y in (11) we have
| (14) |
In (16), let δ = δʹ = δ1, we have fz(δ1) = fx(δ1)
Similarly we have fz(δ2) = fy(δ2)
Let δ = δ1, δʹ = δ2, we show
| (15) |
From 13 and 15 we know that fy(δ2) = fx(δ2), fy(δ1) = fx(δ1). Hence, fx = fy. If Tx = Ty, we can choose z ∈ B/{0} such that Tz≠Tx. Then fx = fz = fy. (ii) follows from first part (i) and 9
Lemma 5: For each x ∈ B/{0}, there exists a linear functional λx: K → F and a symmetric bilinear map σx: K×K → K such that txδ1οtxδ2 = λx(δ2) txδ1 + λx (δ1) txδ2 + σx(δ1, δ2) for all δ1, δ2 ∈ K
Proof: For x, y ∈ B/{0}, by (7) and Lemma 3 and Lemma 4 we have
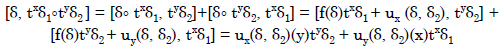 | (16) |
For all d ∈ K. It follows that txδ1οtyδ2 ∈ K + gx + gy.
Let x = y, we have txδ1οtxδ2 ∈ K+gx. Then txδ1οtxδ2 = txδʹ+σx(δ1, δ2) for some symmetric bilinear map σx: K×K → K and δʹ ∈ K. For any d ∈ K, we have [δ, txδʹ1οtxδ2 ] = δ(x)txδʹ. Using 16 we have δ(x)δʹ = ux(δ, δ1)(x)δ2 + ux(δ, δ2)(x)δ1. Fixing δ0 ∈ K such that
for all δ1 ∈ K. It is clear that λx (δ1) does not depend on the choice of δ0 with δ0(x) ≠ 0. So txδ1οtyδ2 = λx(δ1) txδ2 + λ2(δ2) txδ1 + σx(δ1, δ2).
Lemma 6:
| (i) | For any x, y ∈ B/{0}, there exists a bilinear sxy: K´ K → K such that: |
| (ii) | For any δ, δ1 ∈ K, x ∈ B/{0}, δοtxδ1 = f(δ)txδ1 + λx(δ1)δ |
Proof:
| (i) | Let x, y ∈ B/{0} and x ≠ y. For any δ1, δ2 ∈ K we know that txδ1οtyδ2 = txδʹ1+tyδʹ2 + σxy(δ1, δ2) for some δʹ1, δʹ2, σxy(δ1, δ2) ∈ K. It is clear that σxy is a bilinear map from K×K to K. For any δ ∈ K, by [δ, txδ1οtyδ2] = δ(x)txδʹ1 + δ(y)tyδʹ2 and (16) we have δ(x)δ = uy(δ, δ2)(x)δ1 and δ(y) |
we have λxy(δ2) δ(x)txδ1 + λxy(δ1) δ(y)tyδ2-uy(δ, δ2)(x)txδ1-ux(δ, δ1)(y)tyδ2 = 0. Hence
| (17) |
for all δ1, δ ∈ K. Denote λxx = λx, we have that 17 holds for all y ∈ B/{0}
Now we shall prove that λyx = λzx for all x, y, z ∈ B/{0}.
If Ker y = Ker z, since λxy(δ1)δ-ux(δ, δ1)) (y) = 0, we know λxy(δ1)δ - ux(δ, δ1) ∈ Ker y = Ker z and hence (λxy(δ1)δ-ux(δ, δ1))(z) = 0. Then λxy(δ1)δ(z) = ux(δ, δ1)(z) = λzx(δ1)δ(z) for all δ, δ1 ∈ K . Hence λyx = λzx.
If Ker y ≠ Ker z, we can choose δʹ, δʹʹ ∈ K such that δʹ(y) = 1, δʹ(z) = 0, δʹʹ(y) = 0, δʹʹ (z) = 1. By (17), we can show
Let δ = δʹ and δʹʹ, we show
For all d1 ∈ K . Hence, we have λyx = λxx = λx for all x, y ∈ B/{0}.
| (ii) | For any z ∈ B/{0} we have ux(δ, δ1)(z) = λzx(δ1)δ(z) = λx(δ1)δ(z) |
Hence, ux(δ, δ1) = λx(δ1). From Lemma 3 we know (ii) is true.
Lemma 7: For any x, y ∈ B/{0}, x ≠ y and δ1, δ2 ∈ K, we have.
| • | σx(δ1, δ2) = 0, where σx: K×K → K is the symmetric bilinear map defined in Lemma 5 |
| • | σxy(δ1, δ2) = 0, where σxy: K×K → K is the bilinear map defined in Lemma 6 |
Proof: Let x ∈ B/{0}. From [txδ1, txδ1οtxδ1] = 0 for all δ1 ∈ K, we have σx(δ1, δ1)(x) = 0. Since, σx is a symmetric linear map we have σx(δ1, δ2)(x) = 0 for all δ1, δ2 ∈ K.
For δ1, δ2 ∈ K, let y ∈ B/{0, x} and δ3 ∈ K. Since, [tyδ3, txδ1οtxδ2] = [tyδ3οtxδ2, txδ1] + [tyδ3οtxδ1, txδ2], we have σx(δ1, δ2)(y) tyδ3 = σyx(δ3, δ2)(x) txδ1 + σyx(δ3, δ1)(x) txδ2 which implies σx(δ1, δ2)(y) = 0. So σx(δ1, δ2) ∈ K0 = 0. Hence σx(δ1, δ2) = 0 for all δ1, δ2 ∈ K. Similarly, we can prove (ii).
Now we can give the following main theorem of this paper.
Theorem 1: If * is a third power-associative (-1, 1) multiplication on the simple generalized Kac-Moody algebra g, then there exist a linear functional τ: g →![]() such that
such that
| (18) |
for all u, v ∈ g.
Conversely, if * is a multiplication on g defined by (18), then * is a third power-associative (-1, 1) multiplication on g
Proof: Define a linear functional τ: g → ![]() by:
by:
It is clear that (18) is true.
From (1) we have (x * y) * y = x * (y * y) for all x, y ∈ B which is equivalent to [x, y]οy = [x, yοy]. Using theorem 1 we can determine all (-1, 1) multiplication on simple generalized Kac-Moody algebras.