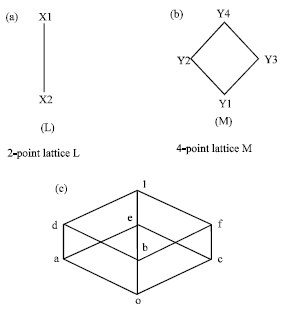
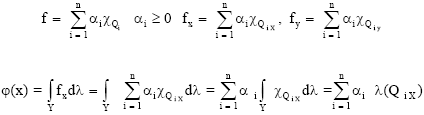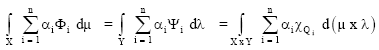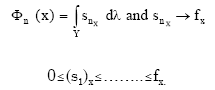Research Article
Characterization of Lattice Measurable Functions on Product Lattices
Nizam Institute of Engineering and Technology, Deshmukhi, Nalgonda District, Hyderabad, A.P., India
T. Nageswara Rao
Mary`s Women`s Engineering College, Budampadu, Guntur Rural, Guntur, A.P., India
J. Venkateswara Rao
Department of Mathematics, Mekelle University, Mekelle, Ethiopia