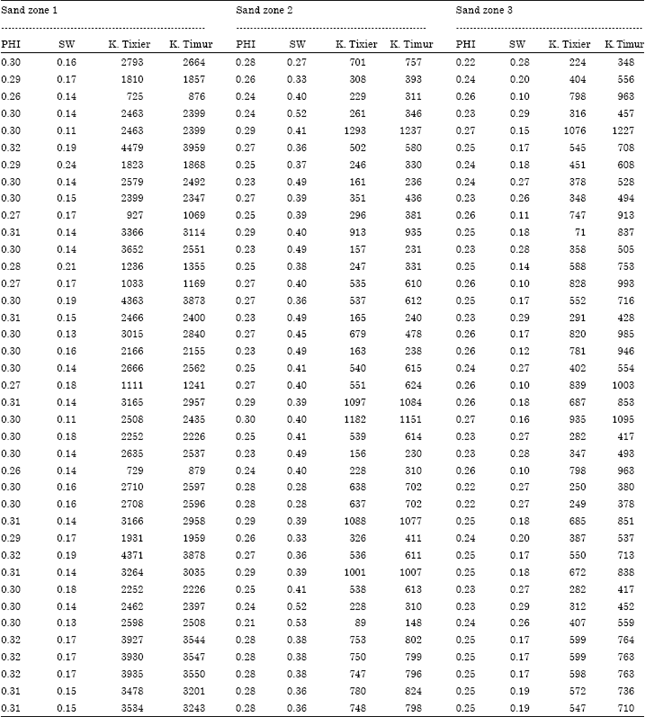
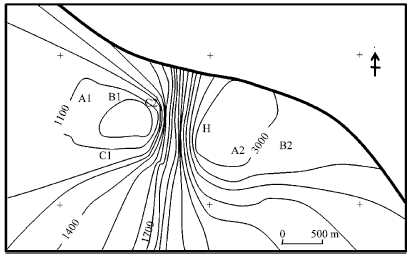
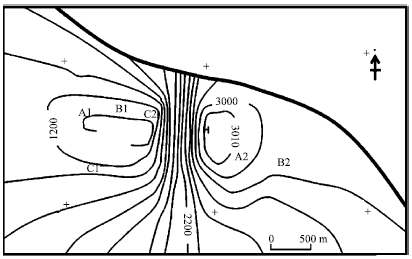
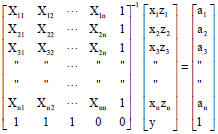Research Article
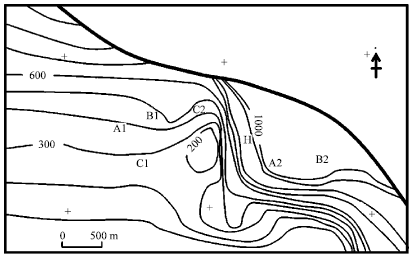
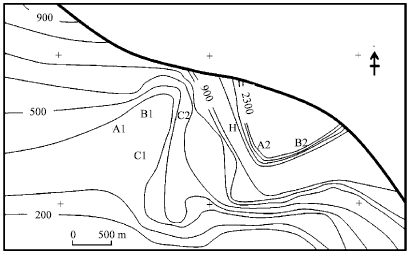
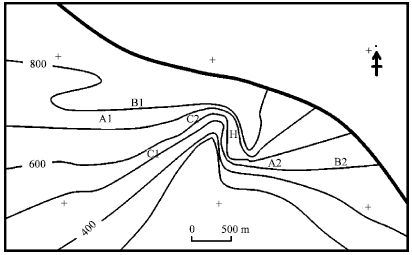
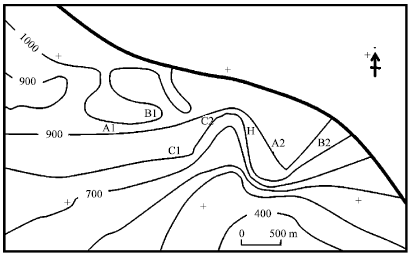
Effectiveness of Kriging Interpolation Technique for Estimating Permeability Distribution of a Field
Department of Physics, Delta State University, Abraka, Nigeria
U. Chapele
Department of Physics, Delta State University, Abraka, Nigeria