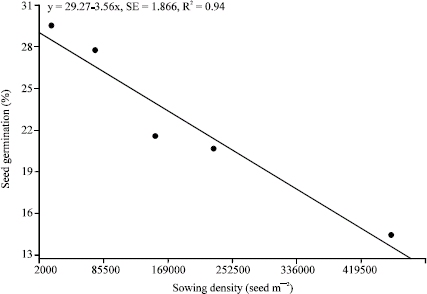
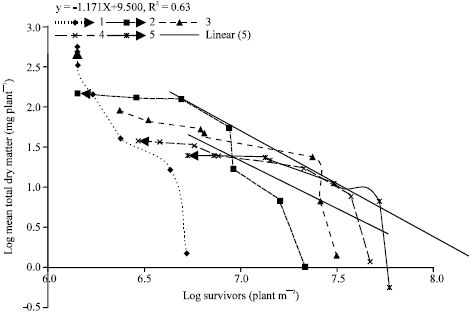
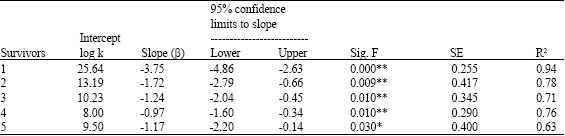
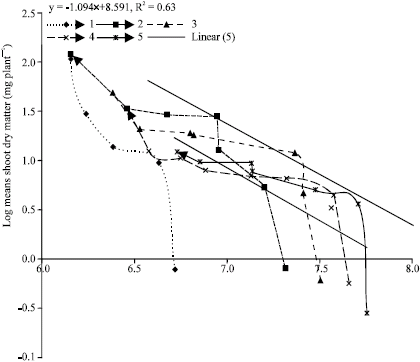
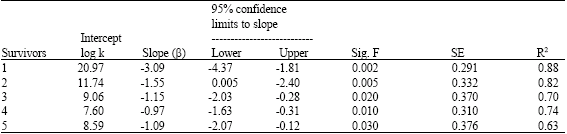
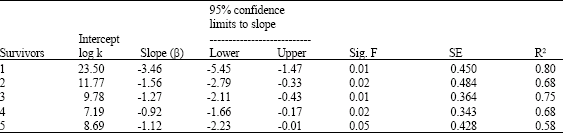
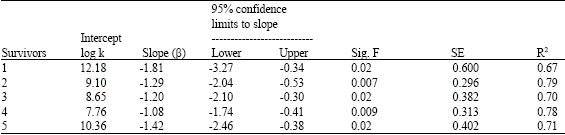
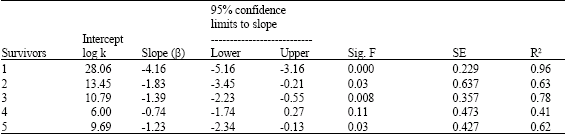
Research Article
Population Structure and its Influence on Self-Thinning of Melastoma malabathricum L.
Institute of Biological Sciences, University of Malaya, 50603, Kuala Lumpur, Malaysia
B.B. Baki
Institute of Biological Sciences, University of Malaya, 50603, Kuala Lumpur, Malaysia