INTRODUCTION

Pricing of securities depends on volatility of each asset. Therefore, price changes indicate the average reaction of investors to news. The arrival of new information makes investors to adapt their expectations and this is the main cause for price and return changes. Trading volume and volatility are indicators of the current stock market activity on one hand and a potential source of information for the future behavior of stock market on the other hand. Numerous papers have documented the fact that high stock market volume is associated with volatile returns. However, many theoretical and empirical studies are designed to work with the conditional variance in developed markets (Dimson and Marsh, 1990; McMillan et al., 2000). Various studies reported that there are significant relationships between volume and stock price movement and volatility. For example, Saatcioglu and Starks (1998) found that volume led stock prices changes in four out of the six emerging markets. Chan et al. (2000) found that trading volume for foreign stocks is strongly associated with NYSE opening price volatility. Griffin et al. (2007) investigated the dynamic relation between market-wide trading activity and returns in 46 markets and reported strong positive relationship between turnover and past returns. Recently, several authors have investigated the volatility of stock market by applying econometric models and suggested that, no single model is superior (Akgiray, 1989; Pagan and Schwert, 1990). Brailsford and Faff (1996) and Koutmos (1998) examined the predictive performance of several statistical methods with GARCH and TGARCH models for Australian stock exchange. Dimson and Marsh (1990) examined various technical methods of predicting the volatility of UK stock market returns and find that exponential smoothening and regression model performed.

The present study reinvestigates the effect of trading volume on volatility of the Nasdaq index in US stock market using GARCH model to see to what extent the stock market’s reaction to the arrival of news changed when trading commenced. Further we also analysis the contemporaneous relationship between stock price volatility and trading volume. Also a few attempts were made to model the most prominent features of the time series of Nasdaq index such as volatility clustering, excess kurtosis and fat tailed by applying the most popular techniques proposed by Engle (1982). To capture the above characteristics, ARCH class of models were introduced by Engle (1982) and GARCH (Generalized Autoregressive Conditional Heteroskedasticity) by Bollerslev (1986) and Taylor (1986). Since the intrinsically symmetric GARCH model does not cope with the asymmetry issues or so called leverage effect, the Exponential Generalized Autoregressive Conditional Heteroskedasticity process (EGARCH) by Nelson (1991) is suggested. Finally, to capture asymmetries in terms of negative and positive shocks TGARCH (Threshold Generalized Autoregressive Conditional Heteroskedasticity) model was introduced by Zakoian (1994) and Glosten et al. (1993).

REVIEW OF LITERATURE

Random walk model: The random walk model is the simplest possible models, where the Ordinary Least Square (OLS) method are constructed on the assumption of constant variance. As per, efficient market hypothesis the competing market participants reflect information instantly hence are useless in predicting future prices. The basic model for estimating stock returns fluctuation by using OLS in the naïve random walk model is given below:

where, μ is the mean value of the returns, it is expected to be insignificantly differ from zero and ε_t is the error term should not be serially correlated over time.

GARCH: Bollerslev (1986) extended Engle’s ARCH model to the GARCH model and it is based on the assumption that forecasts of time varying variance depend on the lagged variance of the asset. An unexpected increase or decrease in returns at time t will generate an increase in the expected variability in the next period. The basic and most widespread model GARCH can be expressed as:

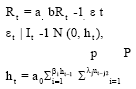where, λ_j>0, β_i = 0. The GARCH is weekly stationery Σβ_i+Σλ_j<1, the latter two quantifying the persistence of shocks to volatility (Nelson, 1991).

In particular, volatility forecast are increased following a large positive and negative index return, the GARCH specification that capturing the well-documented volatility clustering evident in financial returns date (Engle, 1982).

TGARCH: In TGARCH model, it has been observed that positive and negative shocks of equal magnitude have a different impact on stock market volatility, which may be attributed to a leverage effect (Black, 1976). In the same sense, negative shocks are followed by higher volatility than positive shocks of the same magnitude (Engle and Ng, 1993). The threshold GARCH model was introduced by the works of Zakoian (1994) and Glosten et al. (1993). The main target of this model is to capture asymmetric in terms of negative and positive shocks and adds multiplicative dummy variable to check whether there is statistically significant different when shocks are negative. The conditional variance for the simple TGARCH model is defined by:

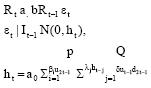where, d_t takes the value of 1 if ε_t is negative and 0 otherwise. So good news and bad news have a different impact.

EGARCH: The Exponential GARCH model specifies conditional variance in logarithmic form, which means that there is no need to impose estimation constraints in order to avoid negative variance Nelson (1991). The mean and variance equation for this model is given by:

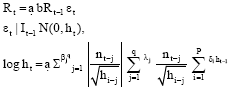where, δ captures the asymmetric effect. The exponential nature of EGARCH ensures that the conditional variance is always positive even if the parameter values are negative; thus there is no need for parameter restrictions to impose non-negativity.

Smirlock and Starks (1985) found that the return-volume relation is asymmetric and later, Smirlock and Starks (1988) found a strong positive lagged relationship between volume and absolute price changes using individual stock data. Lee and Swaminathan (2000) used monthly returns and daily trading volume of all the firms listed on NYSE and American Exchange (AMEX) and find that momentum and trading volume appear to predict subsequent returns in the US equity market. Bekaert and Wu (2000) not only support this finding but also suggest that negative shocks generate a greater response in volatility than positive shocks of an equal magnitude, evidence of the speed of information transmission in markets. Thus, the findings of past studies are strong indications of information content of volatility on the markets, which could be used by investors to earn abnormal profit. Ratner and Leal (2001) examined the Latin American and Asian financial markets and find a positive contemporaneous relation between return and volume in these countries except India. At the same time they observed that there exists a bi-directional causal relation between return and volume. In summary, the return and volume are strongly related contemporaneously but there is little evidence that either can be used to predict the other. De Medeiros and Doornik (2006) investigated the empirical relationship between stock returns, return volatility and trading volume using data from the Brazilian stock market. The study found out there is a contemporaneous and dynamic relationship between return volatility and trading volume and return volatility contains information about upcoming trading volumes. Atmeh and Dobbs (2006) investigated the performance of moving average trading rules in the Jordanian stock market and found that technical trading rules can help to predict market movements. Al-Khouri and Ajlouni (2007) reported that the price-limit technique was effective in reducing the volatility in the Amman stock exchange. Floros and Vougas (2007) used GARCH and GMM method to investigate the relationship between trading volume and returns in Greek stock index futures market and found that trading volume was used as the indicator of prices.

EMPIRICAL RESULTS AND ANALYSIS

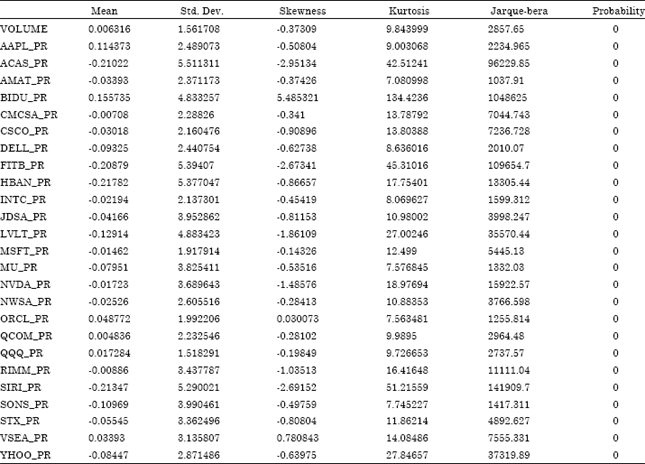
The basic descriptive analysis of the time series of stock returns and trading volume is shown in Table 1. All returns are calculated as the first difference of the log of the daily closing price. Daily trading volume and stock return have positive kurtosis and high JB statistics that implies that the distribution is skewed to the right and they are leptokurtic((heavily tailed and sharp peaked), i.e., the frequency distribution assigns a higher probability to returns around zero as well as very high positive and negative returns. The Jarque-Bera statistic test indicates that the null hypothesis of normality is rejected and shows that all the series exhibit non-normality and indicates the presence of Heteroscedasticity. Hence, GARCH (1, 1) model is the suitable for testing of hypothesis.

The study here employs the unit root test to examine the time series properties of concerned variables. Unit root test describes whether a series is stationary or non-stationary.

Table 1:	Diagnostic tests

Table 2:	Unit root tests

For the test of unit root the present study employees the Augmented Dickey Fuller test and KPSS test (Dickey and Fuller, 1981). ADF test is used to measure the stationarity of time series data which in turn tells whether regression can be done on the data or not. The output is presented in the Table 2. On observing the outputs of ADF and KPSS tests, it is seen that the ADF test statistic and KPSS test statistics for all is less than the critical values at 1, 5 and 10% confidence level. Both ADF and KPSS test statistics confirm that all prices have unit root (non-stationary). So, the null hypothesis is rejected and the data is found to be stationary.

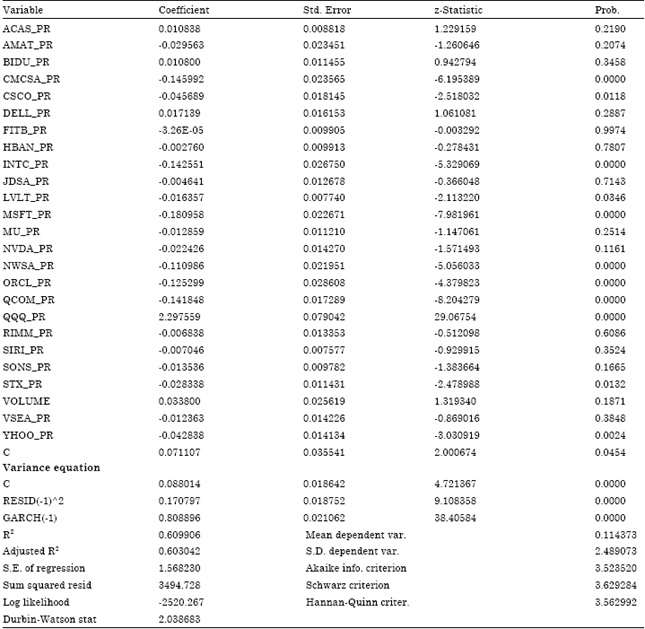
We investigate that weather trading volume has an explanatory power for Indian stock market by fitting GARCH (1, 1) model with daily volume included in the conditional variance equation. It is evident from the Table 3 that parameter β is negative and statistical insignificant indicating that trading volume does not have GARCH effect in the stock market.

Table 3:	GARCH model with trading volume

Systematic variations in trading volume are assumed to be caused only by the arrival of new information. AIC and SIC criteria used in the study indicating lower for the regression which is quite reasonable and fit for our model. Further Durbin-Watson value is 2 suggests autocorrelation or specification errors. Since the Durbin-Watson statistic is greater than 2, the error terms are not auto correlated indicating that the statistical model is fit and appropriate.

LEVERAGE/ASYMMETRIC EFFECT

It is very often observed that downward movement of the markets is followed by higher volatilities than upward movement of the same magnitude. So it is important to use TARCH, EGARCH, PGARCH and component ARCH models to test asymmetric shocks to volatility. Sometimes the simple GARCH models cannot capture some important features of the data.

Table 4:	TARCH model with trading volume

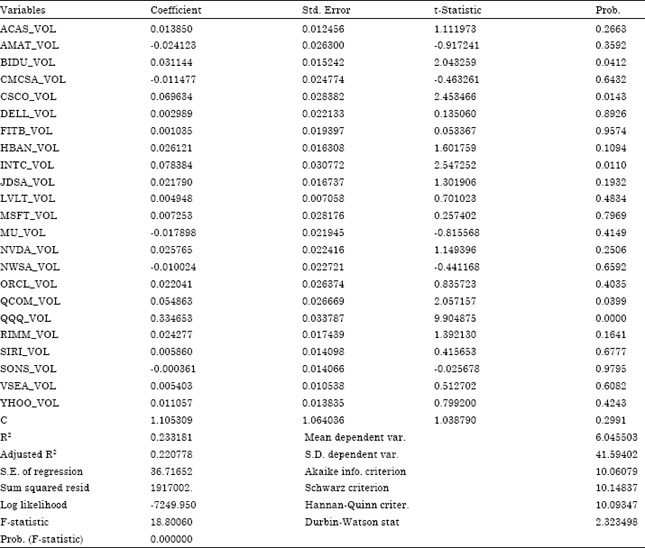To investigate the leverage effect we have used TARCH (1, 1) model introduced independently by Zakoian (1994). If the bad news has a greater impact on volatilities than good news, a leverage effect exists. ARCH model helps to explain the volatility of spot market when some degree asymmetric is present in the data.

TARCH model takes the leverage effect into account. The presence of leverage effect is seen in Table 4 which implies that every price changes are responding asymmetrically to the positive and negative news in the market. In the conditional variance equation; α, the coefficient for latest news which is statistically significant at 1% level indicating that the recent news has an impact on the volatility of the stock. Similarly β coefficient is insignificant and suggests that old news is not influencing the stock market volatility. Coefficient γ (parameter of volume) is positive and greater than 0 indicating the impact is asymmetric. The analysis shows that trading volume is associated with an increase in stock return volatility. Good news therefore induces more trading volume than bad news.

To test the leverage effect, EGARCH model is also used. Table 5 exhibited the existence of leverage effect and news impact is asymmetric (γ).

Table 5:	EGARCH model with trading volume

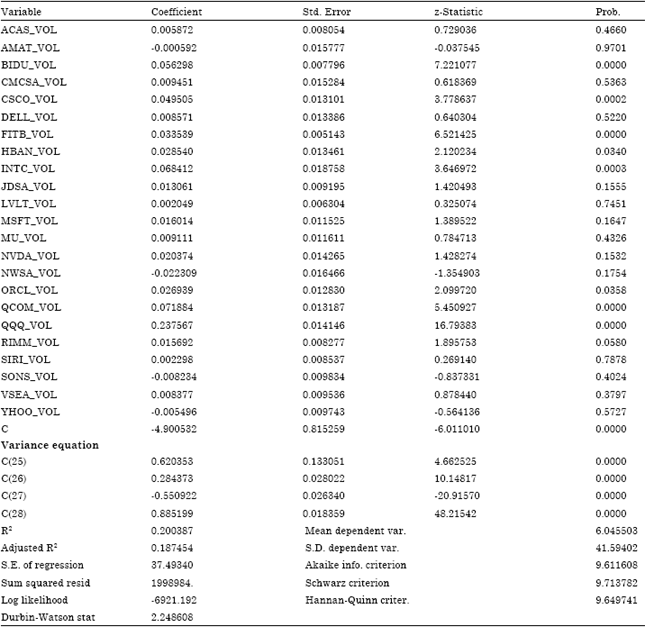As Coefficients γ is positive, greater than 0 and significant at 1% level, the analysis is suggesting that trading volume increases due to good news in the market. Coefficients γ shows a positive impact of volume on stock return also generate less impact on volatility of the market.

The empirical evidence in the Table 5 suggests the existence of leverage effect and news impact is asymmetric (γ). In the models with a significant power parameter we found δ smaller than 2, in concordance with Ding et al. (1993) results and the asymmetric estimated parameter γ is positive. So trading volume increased the stock return and decrease expected volatility in the market. This supports a positive correlation between trading volume and predictable volatility of stock returns. The analysis shows that the PARCH model which exhibits a low power effects but strong leverage effects in the market.

So far we have used TARCH, EGARCH and PARCH model to find the significance of the asymmetric effects. Alternatively it is also equally important to find the cross correlation between the squared standard residuals and lagged standardized residuals to know the impact of long run/short run movements in volatility.

CONCLUSION

This study examined the relationship between stock returns and trading volume and has used the GARCH (1, 1) model, asymmetric TARCH, EGARCH, PGARCH and CARCH model to empirically examine the persistence of shocks to volatility and to determine the asymmetry in the pattern of volatility. This paper specifically tested the hypothesis of variability in volatility, which implies that volatility is greater when stocks price are moving downwards than upwards. Statistical inferences are drawn from the data by means of significance tests and over all goodness of fit of all the models as reported by the Akaike info criterion &Schwarz criterion. The study found that the recent news has an impact on the volatility of the trading volume. Also, the past news coefficient is statistically insignificant and suggests that old news is not having influencing the trading volume volatility. So it is evident from the study that systematic variations in trading volume are assumed to be caused only by the arrival of new information. To predict volatility, we have used the asymmetric TARCH, EGARCH, PARCH and Component ARCH model and evidence suggests that leverage effects exist and the news impact is asymmetric. This implied that daily new information in market may have significant impact on price volatility. So the study concludes that bad news generate more impact on volatility of the stock return and trading volume. One explanation may be that normally investors have a higher aversion to downside risk, so they react faster to bad news.