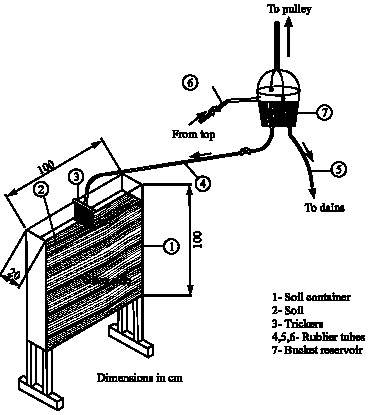
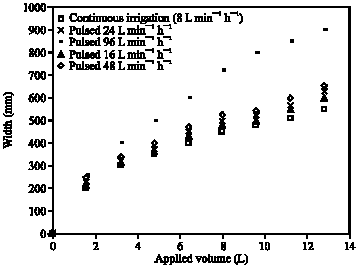
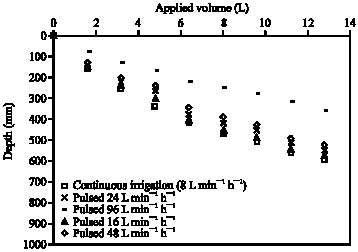
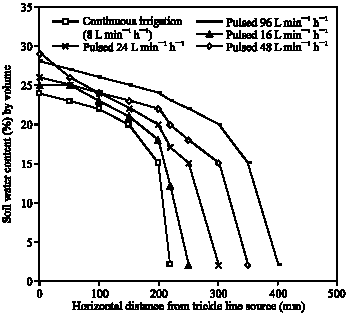
Clinical Report
Use of Pulse Trickles to Reduce Clogging Problems in Trickle Irrigation System in Saudi Arabia
Department of Environmental and Natural AgriculturalResources,
Collage of Agriculture and Food Sciences, King Faisal University,
Hofuf Al-Ahsa, Kingdom of Saudi Arabia