ABSTRACT
In this research, cephalosporin C (CPC) production on pilot scale fermenters of 600 L capacity with 350 L working volume by Acremonium chrysogenum UMIP 2566.04 was performed. The effects of fermentation medium composition, inoculum concentration, initial pH and aeration rate on CPC production was investigated by using Response Surface Methodology (RSM). The Plackett-Burman design which involves two concentrations of each nutrient was effective in searching for the major medium components promoting CPC production. Under our experimental conditions; Soya oil, beet molasses and corn steep liquor were found to be the major factors contributing to the antibiotic production. Subsequently, a Box-Behnken design was used for outlining the concentration of the most effective medium constituents. Estimated optimum composition for the production of CPC was as follows: soya oil, 40 g L-1; beet molasses, 180 g L-1 and corn steep liquor, 330 g L-1. The central composite design was used for outlining the optimum values of the fermentation parameters. Estimated optimum values for the production of CPC are as follows: inoculum level, 105.5 spores mL-1; initial pH, 4.3 and aeration rate, 9364 L min-1.
PDF Abstract XML References
How to cite this article
URL: https://scialert.net/abstract/?doi=jm.2007.1.12
INTRODUCTION
β-lactam antibiotics are the most important antibiotics from the medical, economic and academic points of view. They are the most potent and least toxic of all the known antibiotics. Cephalosporins are β-lactam antibiotics containing a dihydrothiazine ring with D-α-aminoadipic acid. Cephalosporins are less toxic and broad-spectrum antibiotics comparable in action to ampicillin. They are effective against Gram-positive and Gram-negative bacteria (Adinarayana et al., 2003).
The optimization of fermentation conditions are of primary importance in the development of any fermentation process owing to their impact on the economy and practical feasibility of the process. The diversity of combinational interactions between fermentation parameters and productivity do not permit satisfactory detailed modeling. The one-dimensional search with successive variation in variables such as the one variable at a time approach (OVAT) is still employed, even though it is well accepted that it is practically impossible for the one-dimensional search to accomplish an appropriate optimum in a finite number of experiments. Single variable optimization methods are not only tedious, but also can lead to misinterpretation of results, especially because the interaction between different factors is overlooked (Haltrich et al., 1994; He et al., 2004).
Statistical experimental designs have been used for several decades and it can be adopted at various phases of an optimization strategy, such as for screening experiments or for looking for the optimal conditions for targeted response(s) (Box and Behnken, 1960). Fermentation optimization using a statistically planned experiment is a sequential process (Box et al., 1978; Haaland, 1989). First, a large number of continuous factors (typically 5 to 12) are screened and insignificant ones are eliminated in order to obtain a smaller, more manageable set of factors. The remaining factors could be optimized by a response surface modeling methodology. Finally, after model building and optimization, the predicted optimum is verified experimentally (Swanson et al., 1986; Strobel and Nakatsukasa, 1993).
The present study aimed to optimize the production of cephalosporin C (CPC) by three optimization approaches. The first and second approaches were applied to determine the optimal media composition using the Plackett-Burman and Box-Behnken designs. The third approach was performed to find out the optimal levels of the fermentation parameters: inoculum level, initial pH and aeration rate as independent variables by using the central composite design (Mason et al., 1989). In an attempt to reduce the raw materials costs amount which represent approximately 60% of industrial product formation costs (Seidel et al., 2002), beet molasses was utilized as a novel carbon source for CPC production.
MATERIALS AND METHODS
Strain
The organism used throughout this study is a new Egyptian soil Acremonium chrysogenum isolate deposited in Pasteur Institute (Fungi Culture Collection) Paris, France. The number of the strain is UMIP 2566.04.
Inoculum
Spores suspension of fungal strain was prepared by washing 5 days old culture slants with sterilized saline solution (0.9% NaCl) and shaking vigorously for 1 min. Spores concentration was adjusted to approximately 108 spores mL-1.
Basal Fermentation Medium
A medium of the composition (g L-1): KH2PO4 3.1; ZnSO4 0.02; corn steep liquor, 110; NH4SO4, 4.2; Na2SO4, 5.0; soya oil, 40; CuSO4, 0.02; MgSO4, 0.67; L-methionine, 20; beet molasses, 60; urea, 2.1 (pH 6±0.2) was used as the basal medium.
Batch Fermentation
Inoculum level of 5% (V V-1) was transferred to air lift double-jacket pilot fermenters (Belach Bioteknik) of 600 L capacity with 350 L working volume. The fermenters are made entirely of stainless steel AISI 316. The incubation temperature, initial pH and aeration were carried out at 25°C, 6.0 and 6500 L min-1, respectively. Contramine® was automatically dosed to avoid foaming during the fermentation. The fermenters were provided with separated adjustable air compression systems to generate constant sterile air flow which maintains a constant level of dissolved oxygen in the fermenter. Sterile air was introduced into the fermenters through small spargers to ensure adequate aeration of the fermentation medium. The outlets of the fermenters were constructed to preclude contamination. Each fermenter possesses two openings for the insertion of calibrated pH and temperature probes to monitor both pH and temperature during the fermentation run. When the elapsed time (180 h) for a fermentation run ended, the fermenter was discharged, washed, rinsed with distilled water and sterilized. The fungus was allowed to grow for the requisite time under the experimental conditions. Thereafter, biomass was isolated by centrifugation at 5000 rpm for 10 min and the supernatants were separated to carry out the necessary analyses.
Determination of CPC and Sugar Concentrations
CPC concentration was determined using a packed column with Nuckeosil 5® with reverse phase mode operated at 30°C with a mixture of 5% methanol, 95% of 14 mM phosphate buffer and 10.2 mM tetrabutyl ammonium hydrogen sulphate (TBAHS) pH 6.5 as eluent. Glucose and fructose were determined by using Aminex HPX-87P® column operated at 40°C. The eluent used for analysis was 0.01N sulfuric acid solution. HPLC analyses were carried out under the following operation conditions: pump flow, 0.6 mL min-1; sample amount, 20 μL and integration method, peak area using Gilson HPLC equipped with UV-detector (for CPC) and RI-detector (for glucose and fructose). Concentrations were automatically calculated by Gilson Unipoint software. Sugar concentration was calculated as the sum of glucose and fructose concentrations.
Experimental Designs
Plackett-Burman Design
For screening purpose, eleven independent variables were screened in twelve combinations (Table 1) organized according to the Plackett and Burman design (1946). All trials were performed in triplicate and the average of CPC yield observations were treated as responses. The main effect of each variable was simply calculated as the difference between the average of measurements made at the high setting (+) and the average of measurements observed at the low setting (-) of that factor.
Plackett-Burman experimental design is based on the first order model:
Z = bο + ∑bixi |
Where Z is the response (CPC yield), b° is the model intercept and bi is the linear coefficient and xi is the level of the independent variable. This model does not describe interaction among factors and it is used to screen and evaluate the important factors that influence the response.
Box-Behnken Design
In order to describe the nature of the response surface in the experimental region and elucidate the optimal concentrations of the most significant independent variables, a Box-Behnken design (Box and Behnken, 1960; He et al., 2004) was applied which is a RSM. As presented in Table 2, factors of highest confidence levels namely; soya oil (X1), beet molasses (X2) and corn steep liquor (X3) were prescribed into three levels (low, basal, high) coded, (-, 0, +).
| Table 1: | Plackett-Burman design for 11 variables and 12 trials |
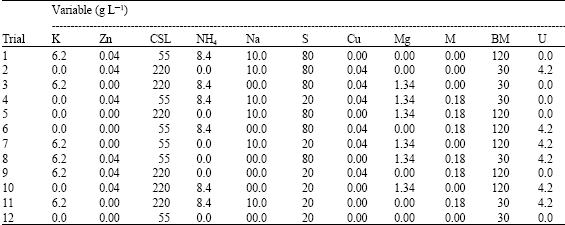 | |
| K, KH2PO4; Zn, ZnSO4; CSL, corn steep liquor; NH4, NH4SO4; Na, Na2SO4; S, soya oil; Cu, CuSO4; Mg, MgSO4.7H2O; M, L-methionine; BM, beet molasses; U, urea | |
| Table 2: | Box-Behnken design and observations for three independent variables: soya oil (X1), beet molasses (X2) and corn steep liquor (X3) |
 | |
| Table 3: | Central composite design and observations for three independent variables: inoculum level (spores mL-1), Y1; initial pH, Y2; and aeration rate (L min-1), Y3 |
 | |
According to the applied design, fifteen combinations were executed and their observations were fitted to the following second order polynomial model:
Z = bo + b1X1 + b2X2 + b3X3 + b11X12 + b22X22 + b33X32 |
Where, Z is the dependent variable (CPC yield); X1, X2 and X3 are the independent variables as mentioned above; bo is the regression coefficient at center point; b1, b2 and b3 are linear coefficients; and b11, b22 and b33 are quadratic coefficients.
The values of the coefficients as well as the optimum concentrations were calculated using Statistica software. The quality of fit of the polynomial model equation was expressed by the coefficient of determination, R2. Experiments were performed in triplicate and mean values are given.
The Central Composite Design
Fermentation factors affecting CPC production were optimized using the central composite design which is a response surface methodology (Box and Draper, 1987; Mason et al., 1989). Three variables,
namely; level of inoculum (Y1), initial pH (Y2) and aeration rate (Y3) were included in the model. Each factor was examined at five different levels (relatively low, low, basal, high, relatively high) coded (--, -, 0, +, ++) as shown in Table 3. According to the applied design, sixteen combinations were executed and their observations were fitted to the following second order polynomial model:
Z = bo + b1Y1 + b2Y2 + b3Y3 + b12Y1Y2 + b13Y1Y3 + b23Y2Y3 + b11Y12 + b22Y22 + b33Y32 |
Where, Z is the dependent variable (CPC yield); Y1, Y2 and Y3 are the independent variables as mentioned above; b0 is the regression coefficient at center point; b1, b2 and b3 are linear coefficients; b12, b13 and b23 are second order interaction coefficients and b11, b22 and b33 are quadratic coefficients.
The values of the coefficients, the optimum levels as well as R2 were determined as mentioned above.
RESULTS AND DISCUSSION
Screening the Significance of Fermentation Medium Components
The design was applied with 12 different fermentation conditions as shown in Table 1. The basal medium described in the materials and methods section was used as the (0) level. A concentration of zero was chosen as the (-1) level for each medium component. The main effect results of each medium constituent and the observations of the Plackett-Burman experimental design were presented in Fig. 1 and Table 4, respectively.
In the range of the examined levels of variables, it is apparent from Fig. 1 that, KH2PO4, corn steep liquor, soya oil, L-methionine, beet molasses and urea showed positive main effects. Soya oil, beet molasses and corn steep liquor were the most significant variable that increased CPC production. On the other hand, ZnSO4, NH4SO4, Na2SO4, CuSO4 and MgSO4 showed negative main effects with different values. Consequently, these constituents were excluded from the fermentation medium as they stand for additional concentrations over the optimal range. A simplified medium of the following composition (g L-1) was expected to be close to optimal levels: soya oil, 80; beet molasses, 120; corn steep liquor, 220. Soya oil contains different amino acids such as cysteine, isoleucine, leucine, lysine, methionine, phenyl alanine, threonine, tyrosine and valine (El-Refai et al., 1986; Martin and Demian, 2002). The biosynthesis of CPC begins by the condensation of three amino acids, L-aminoadipic acid, L-cysteine and L-valine, to form the tripeptide δ-(L-aminoadipyl)-L-cysteinyl-D-valine (LLD-ACV) by the ACV synthetase enzyme (Martin and Demian, 2002). Methionine has long been known as the major stimulant of the formation of Acremonium chrysogenum arthrospores which is correlated with CPC production (Martin and Demian, 2002).
| Table 4: | Observations of the Plackett-Burman experiment |
 | |
| Abbreviations: K, KH2PO4; Zn, ZnSO4; CSL, corn steep liquor; NH4, NH4SO4; Na, Na2SO4; S, soya oil; Cu, CuSO4; Mg, MgSO4.7H2O; M, L-methionine; BM, beet molasses; U, urea | |
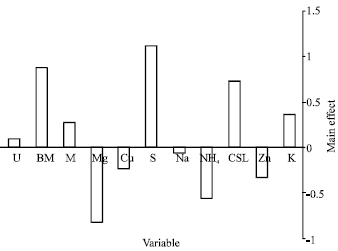 | |
| Fig. 1: | The main effects of the fermentation medium constituents on CPC production according to the Plackett-Burman experimental results. Abbreviations: K, KH2PO4; Zn, ZnSO4; CSL, corn steep liquor; NH4, NH4SO4; Na, Na2SO4; S, soya oil; Cu, CuSO4; Mg, MgSO4.7H2O; M, L-methionine; BM, beet molasses; U, urea |
Methionine also induces four of the enzymes of CPC biosynthesis at the level of transcription (Martin and Demian, 2002). Beet molasses, a by-product of beet sugar industry, contains sucrose which support slower growth than glucose but a higher rate of specific productivity (Vicik et al., 1990). In addition, it contains trace elements such as, potassium, sodium, calcium, zinc, iron and copper (El-Abyad et al., 1992) that may act as macro or micro nutrient for the fungal strain. Corn steep liquor, a by-product of corn wet milling, was used by many investigators as a medium component for CPC production (Jurgens et al., 2002; Seidel et al., 2002).
As certain factors were eliminated due to lack of significance on the basis of the calculated t-values and confidence level (%), soya oil, beet molasses and corn steep liquor were retained and examined more thoroughly. According to these results, a simplified medium of the following composition (g L-1) is expected to be near optimum: soya oil, 80; beet molasses, 120 and corn steep liquor, 220. When these variable levels were applied in a confirmatory experiment approximately 1.34 fold-increase in CPC yield was achieved when compared to the results obtained by the basal culture (data not shown).
Subsequently, a RSM was performed according to Box and Behnken (Box and Behnken, 1960) for further investigation of significant independent variables soya oil, beet molasses and corn steep liquor.
Optimization of Medium Constituents Concentration by Box-Behnken Design
In order to approach the optimum response region of CPC yield, significant independent variables (soya oil, beet molasses and corn steep liquor) were further explored, each at three levels. Table 2 represents the design matrix of the coded variables together with the experimental results of CPC yield (mg CPC g substrate-1). All cultures were performed in triplicate and the average of the observations was used. The optimization results were analyzed both mathematically and graphically. The mathematical solution was carried out with the help of Statistica software by the linear optimization method. Solving the model according to the data obtained from Table 2 revealed an optimum response at the following concentrations (g L-1): soya oil, 40; beet molasses, 180 and corn steep liquor, 330 with a predicted CPC yield of 213.35 mg CPC g substrate-1. Another method to find out the solution was the graphical method, illustrated in Fig. 2, which was applied with the help of the software Statistica to generate a three-dimensional draw of the polynomial equations.
 | |
| Fig. 2: | The response surface of CPC yield (mg CPC g substrateG1) as a function of corn steep liquor (g LG1), soya oil (g LG1) and beet molasses (g LG1) based on the Box-Behnken experimental results |
Presenting experimental results in the form of surface plots Fig. 2a describes the effects of beet molasses (g L-1) and soya oil (g L-1) concentrations on CPC yield (mg CPC g substrate-1). The maximum value of CPC yield was clearly located at the optimum concentrations of beet molasses and corn steep liquor of 180 and 330 g L-1, respectively. Figure 2b and c show the response surface plot for CPC yield as a function of corn steep liquor concentration (g L-1) and soya oil concentration (g L-1) and corn steep liquor concentration (g L-1) and beet molasses concentration (g L-1), respectively. A positive effect of adjusting the concentrations of the three variables can be observed.
In order to verify the optimization results, an experiment was performed under the predicted optimal condition, where the CPC yield was estimated. The basal fermentation medium, before applying the optimization process of the Box-Behnken experiment, was used as a control. A significant difference in CPC yield appeared after decreasing soya oil concentration to 40 g L-1 instead of 80 g L-1, increasing beet molasses concentration to 180 g L-1 instead of 120 g L-1 and increasing the concentration of corn steep liquor to 330 g L-1 instead of 220 g L-1. The calculated optimum concentrations of the three variables were predicted to attain a maximum CPC yield of 213.35 mg CPC g substrate-1. A verification experiment performed under these optimal conditions showed an actual maximum CPC yield of 215.72 mg CPC g substrate-1 which is approximately 212% greater than that produced by the control culture prepared according to the results of the Plackett-Burman experiment (data not shown). The statistical analysis of the design shows a high precision of the polynomial model that reflects high degree of fitting between predicted and experimental data. This great similarity between the predicted and observed results reflects the accuracy and applicability of the Box-Behnken model in the optimization processes (Bloor and England, 1991; Teruel et al., 1997; Kimmel et al., 1998).
According to these results, the optimized medium formula is composed of soya oil, 40 g L-1; beet molasses, 180 g L-1 and corn steep liquor, 330 g L-1. These factors were estimated using the following second order polynomial model fitted to the obtained results:
Z = 353.69-1.95X1-1.007X2-0.82X3 + 0.012X12 + 3.8 x 10-3 X22 + 2.27 x 10-3 X32 |
Where: Z is the yield of CPC (mg CPC g substrate-1) and X1, X2 and X3 are concentrations (g L-1) of soya oil, beet molasses and corn steep liquor, respectively.
The coefficient of determination R2, which was found to be 0.94, indicating that 94% of the variability in the response can be explained by the model. This revealed that the equation is a suitable model to describe the response of the experiment.
Optimization of Inoculum level, Initial pH and Aeration Rate by the Central Composite Design
The third optimization approach was carried out by applying the central composite design for optimization of inoculum level (spores mL-1), initial pH and aeration rate (L min-1). All cultures were performed in triplicate and the average of the observations was used. The model parameters were estimated with the help of Statistica software according to the data obtained from Table 3. The model revealed an optimum response at the following conditions: spores concentration, 105.5 spores mL-1; initial pH, 4.3; and aeration rate, 9363 L min-1 with a predicted CPC yield of 242.6 mg CPC g substrate-1.
Figure 3 shows the response surface plot for CPC yield (mg CPC g substrate-1). By moving along the X and Y axes, it can be demonstrated that increasing the levels of inoculum (spores mL-1), initial pH and aeration rate (L min-1), has a conspicuous effect on overall linkage. In order to verify the optimization results, an experiment was performed under the predicted optimal conditions, where the CPC yield was the main response. The basal fermentation condition, before applying the optimization process of the central composite, was used as a control: spores concentration, 108 spores mL-1, initial pH, 6.0 and aeration rate, 6000 L min-1. The optimized fermentation conditions recorded a CPC yield of 244.5 mg CPC g substrate-1, which is approximately 114.6% greater than the control culture prepared according to the results of the Box-Behnken experiment (data not shown).
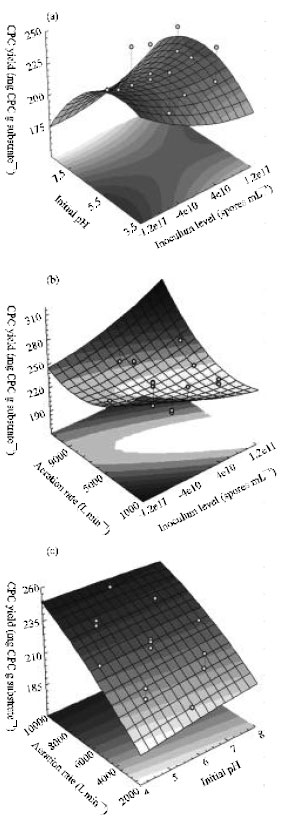 | |
| Fig. 3: | The response of CPC yield (mg CPC g substrateG1) as a function of inoculum level (spores mLG1), initial pH and aeration rate (L min G1) based on the central composite experimental results |
The great similarity between the predicted and observed results reflects the accuracy and applicability of the central composite model in the optimization processes.
According to these results, the suggested optimized fermentation parameters include inoculum level, 105.5 spores mL-1; initial pH, 4.3 and aeration rate, 9363 L min-1. These factors were estimated using the following second order polynomial model fitted to the obtained results:
Z = 162.58+2.08Y1-0.04Y12+3.02Y2-0.09Y22+0.01Y3-2.3x 10-7Y32-0.01Y1Y2-1.3x10-4Y1Y3 - 2x10-4Y2Y3 |
Where: Z is the yield of CPC (mg CPC g substrate-1), Y1 is the inoculum level (spores mL-1), Y2 is the initial pH and Y3 is the aeration rate (L min-1).
The central composite design is an extremely powerful statistical method, since interactions between factors as well as quadratic effects (curvature) are taken into account and quantified in addition to the examination of each factor at five different levels (Parekh et al., 2000). The optimal response region of the examined factors was predicted by using a second order polynomial model fitted to the results obtained by applying the design. The value of determination coefficient R2 = 0.99 for CPC yield indicates that only 1% of the total variations are not explained by the model. The multiple correlation coefficient R was 0.995 for CPC yield. This value indicates a high degree of correlation between the predicted and experimental data.
The RSM designs applied in our investigation have been successfully applied in many recent biotechnological applications (Haltrich et al., 1993; Techapun et al., 2002; Techapun et al., 2003), however to the best of our knowledge no single report was obtained on CPC optimization processes. A maximum CPC yield of 244.5 mg CPC g substrate-1 was reached which is higher than the yield obtained using the OVAT method by many other investigators (Jurgens et al., 2002; Seidel et al., 2002; Adinarayana et al., 2003). We also report for the first time beet molasses as a novel carbon source for CPC production by A. chrysogenum to reduce the cost of the industrial process.
CONCLUSIONS
In screening the factors affecting production of certain metabolite, it is very important to test as many factors as possible and to identify the significance of each of them. Plackett-Burman design offers good and fast screening procedure and mathematically computes the significance of large number of factors in one experiment, which is time saving and maintain convincing information on each component. Although, otherwise, interaction is not included in this design, it is not of first priority in the screening program to examine the interaction between these large numbers of variables. Of these, only the most effective factors with positive significance would be selected for further optimization, while those showing high negative effect on the bioprocess may be dropped in all further experiments.
Applying Box-Behnken and the central composite designs in the optimization process for maximal production is an efficient method that tests the effect of factors interaction. Besides, they convert the bioprocess factor correlations into mathematical models that predict where the optimum is likely to be located. It is worthwhile to advise the microbial industry sponsors to apply such experimental designs to maintain high efficiency and profit bioprocesses.
ACKNOWLEDGMENT
The author would like to acknowledge the Egyptian Danish Company, 6th of October city, Egypt for providing the pilot scale fermenters used in the study.
REFERENCES
- Adinarayana, K., T. Prabhakar, M. Srinivasulu, M.A. Rao, P.J. Lakshmi and P. Ellaiah, 2003. Optimization of process parameters for cephalosporin C production under solid state fermentation from Acremonium chrysogenum. Process Biochem., 39: 171-177.
Direct Link - Bloor, S. and R.R. Ebgland, 1991. Elucidation and optimization of the medium constituents controlling antibiotic production by cyanobacerium Nostoc muscorum. Enzyme. Microb. Technol., 13: 76-80.
Direct Link - Box, G.E.P. and D.W. Behnken, 1960. Some new three level designs for the study of quantitative variables. Technometrics, 2: 455-475.
CrossRefDirect Link - El-Abyad, M.S., F.A. Hamissa and A.S. Gad, 1992. Treatement of beet molasses for citric acid production by a potent strain of Aspergillus niger van Tieghem. Bioresour. Technol., 39: 191-197.
Direct Link - EL-Refai, A.H., K.M. Ghanem and M. Elgazaerly, 1986. Single cell protein production from beet molasses. Microbios, 46: 95-102.
Direct Link - Haltrich, D., M. Preiss and W. Steiner, 1993. Optimization of a culture medium for increased xylanase production by a wild strain of Schizophyllum commune. Enzyme Microb. Technol., 15: 854-860.
Direct Link - Haltrich, D., B. Lavssamayer and W. Steiner, 1994. Xylanase formation by Sclerotium rolfsii effect of growth substrates and development of a culture medium using statistical designed experiments. Applied Microbiol. Biotechnol., 42: 522-530.
Direct Link - He, G.Q., Q.H. Chen, X.J. Ju and N.D. Shi, 2004. Improved elastase production by Bacillus sp. EL31410-further optimization and kinetics studies of culture medium for batch fermentation. J. Zhejiang Univ. Sci., 5: 149-156.
Direct Link - Kimmel, S.A., R.F. Roberts and G.R. Ziegler, 1998. Optimization of exopolysaccharide production by Lactobacillus delbrueckii sub sp. Bulgaricus RR grown in a semidefined medium. Applied Environ. Microbiol., 64: 659-664.
Direct Link - Martin, J.F. and A.L. Demian, 2002. Unraveling the methionine-cephalosporin puzzle in Acremonium chrysogenum. Trends Biotechnol., 20: 502-507.
Direct Link - Parekh, S., V.A. Vinci and R.J. Strobel, 2000. Improvement of microbial strains and fermentation processes. Applied Microbiol. Biotechnol., 54: 287-301.
PubMedDirect Link - Plackett, R.L. and J.P. Burman, 1946. The design of optimum multifactorial experiments. Biometrika, 33: 305-325.
CrossRefDirect Link - Seidel, G., C. Tollnick, M. Beyer, Y. Fahimi and K. Schugerl, 2002. Process engineering aspects of the production of cephalosporin C by Acremonium chrysogenum. Part I. Application of complex media. Process Biochem., 38: 229-239.
Direct Link - Strobel, R.J. and W.M. Nakatsukasa, 1993. Response surface for optimizing Saccharopolyspora spinosa, a novel macrolide producer. J. Ind. Microbiol., 11: 121-127.
Direct Link - Swanson, T.R., J.O. Carroll, R.A. Britto and D.J. Duhart, 1986. Development and field confirmation of a mathematical model for amyloglucosidase/pullulanase saccharification. Starch, 38: 382-387.
CrossRefDirect Link - Techapun, C., T. Charoenrat, M. Watanabe, K. Sasaki and N. Poosaran, 2002. Optimization of thermostable and alkaline-tolerant cellulase-free xylanase production from agricultural waste by thermotolerant Streptomyces sp. Ab106, using the central composite experimental design. Biochem. Eng. J., 12: 99-105.
Direct Link - Techapun, C., N. Poosaran, M. Watanabe and K. Sasaki, 2003. Optimization of aeration and agitation rates to improve cellulase-free xylanase production by thermotolerant Streptomyces sp. Ab106 and repeated fed-batch cultivation using agricultural waste. J. Biosci. Bioeng., 95: 298-301.
CrossRefDirect Link - Teruel, M.L., E. Gontier, C. Bieneime, J.E.N. Saucedo and J.N. Barbotin, 1997. Response surface analysis of chlortetracycline and tertracycline production with k-carrageenan immobilized Streptomyces aureofaciens. Enzyme. Microb. Technol., 21: 314-320.
Direct Link - Vicik, S.M., A.J. Fedor and R.W. Swartz, 1990. Defining an optimal carbon source/methionine feed strategy for growth and cephalosporin C formation by Cephalosporium acremonium. Biotechnol. Prog., 6: 333-340.
Direct Link








