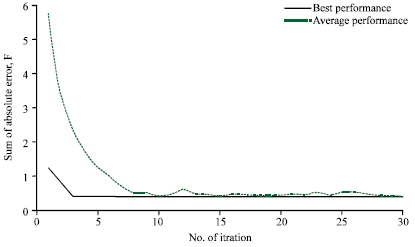
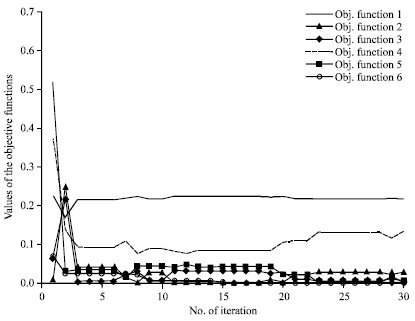
Research Article
Learning Logic Programming in Radial Basis Function Network via Genetic Algorithm
School of Mathematical Sciences, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia
Saratha Sathasivam
School of Mathematical Sciences, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia
Surafel Luleseged Tilahun
School of Mathematical Sciences, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia
Ong Hong Choon
School of Mathematical Sciences, Universiti Sains Malaysia, 11800 USM, Penang, Malaysia