Research Article
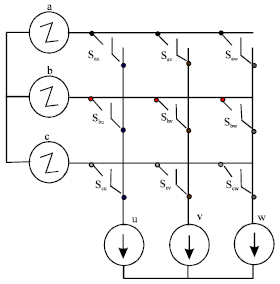
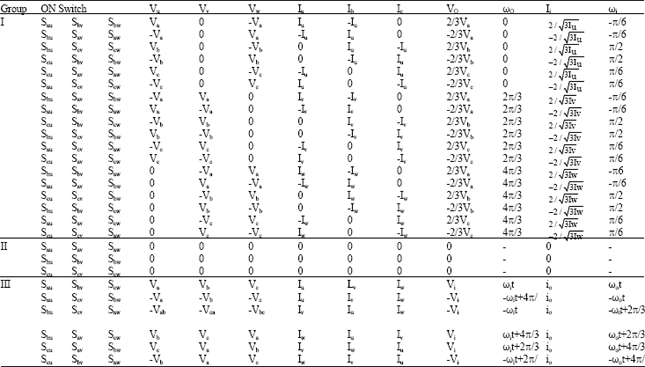
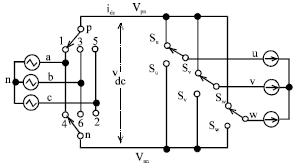
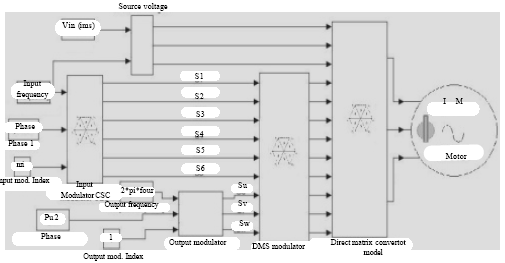
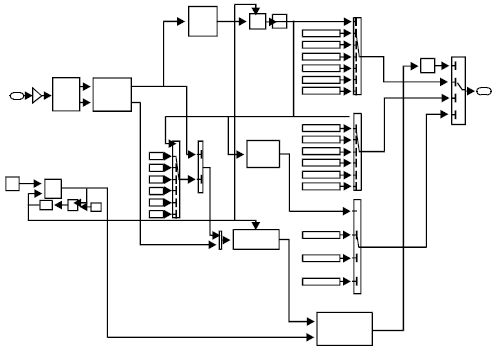
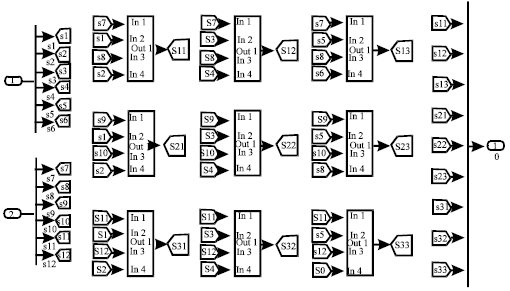
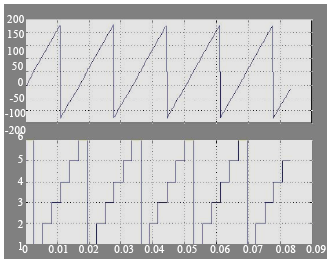
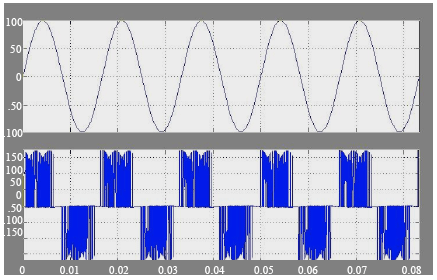
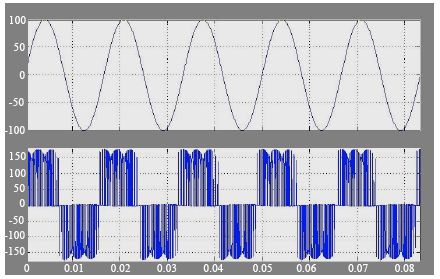
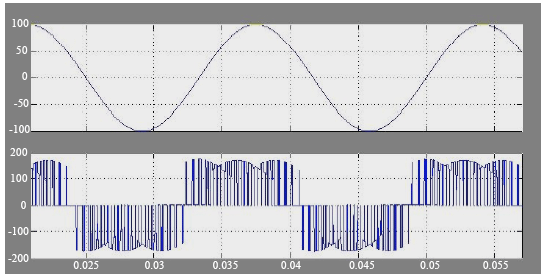
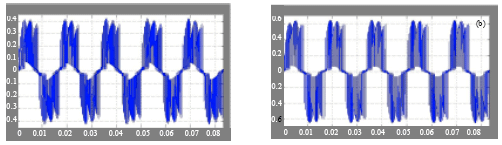
Simulation Model of Space Vector Modulated Control Matrix Converter-fed Induction Motor
Faculty of Electrical and Electronic Engineering, University Malaysia Pahang, Pekan26600, Malaysia
Ruzlaini Ghoni
Faculty of Electrical Automation Engineering Technology, TATiUC24000, Terengganu, Malaysia
N. F. Zakaria
Faculty of Electrical and Electronic Engineering, University Malaysia Pahang, Pekan26600, Malaysia









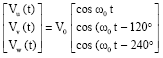
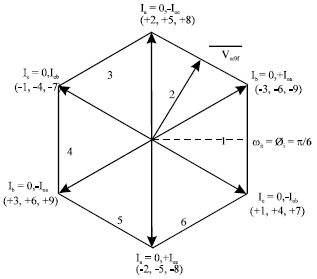


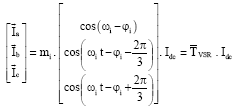

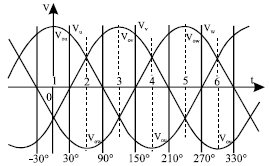


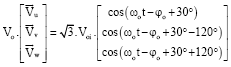


arash firoozi Reply
hello
i need your simulation ( Space Vector Modulated Control Matrix Converter-fed)
pleas send for me
thanks
pouria mohtasham Reply
I need the simulation ,too-I will be grateful if you mail it to me:-)
Nguyen Gia Hoang Anh Reply
hi!Now, I am reseaching this subject, I need your simulation please send for me, Thank so much.
Zachary Reply
Hi,
I am also doing research in this subject but I just started and I need your simulation.
Thanks,
Zachary
C.RAJESHKUMAR Reply
Hi Sir, I am C.RAJESHKUAMR., ME(power electronics student) for my final year project i would like to do your topic with fuzzy control,so i need your simulation for my reference sir,,So please send me if you are willing to provide me.
thank you sir,
best regards,
C.RAJESHKUMAR
manoj Reply
hello i need your simulation ( Space Vector Modulated Control Matrix Converter-fed) pleas send for me thanks