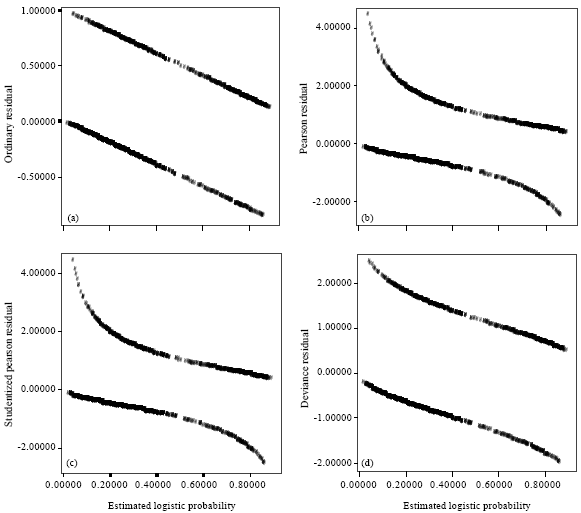
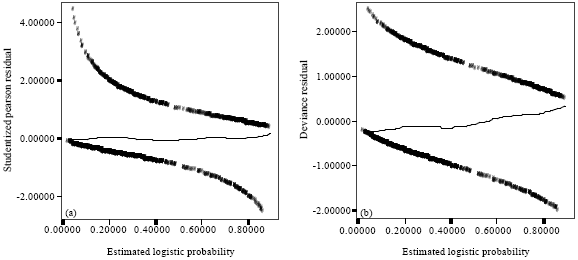
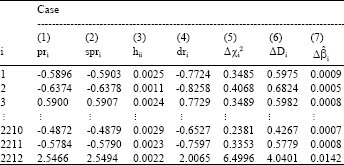
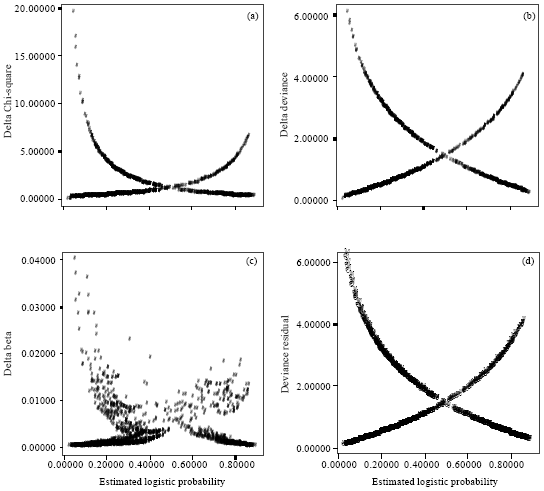
Research Article
Detection of Outliers and Influential Observations in Binary Logistic Regression: An Empirical Study
Laboratory of Applied and Computational Statistics, Institute for Mathematical Research, Universiti Putra Malaysia, 43400 UPM Serdang, Selangor, Malaysia
Habshah Midi
Faculty of Science, Universiti Putra Malaysia, 43400 UPM Serdang, Selangor, Malaysia
Sohel Rana
Laboratory of Applied and Computational Statistics, Institute for Mathematical Research, Universiti Putra Malaysia, 43400 UPM Serdang, Selangor, Malaysia