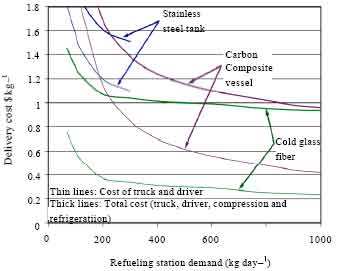
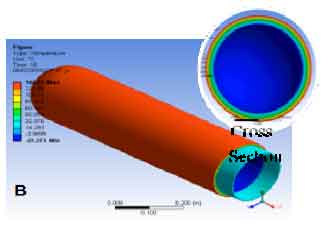
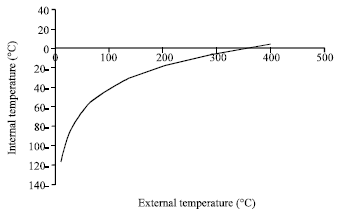
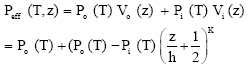Research Article
Numerical Analysis of Thermal and Elastic Stresses in Thick Pressure Vessels for Cryogenic Hydrogen Storage Apparatus
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
H. H. Al-Kayiem
Department of Mechanical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia