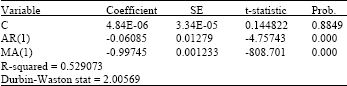
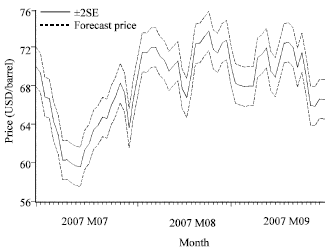
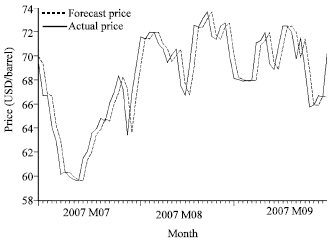
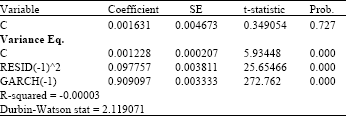
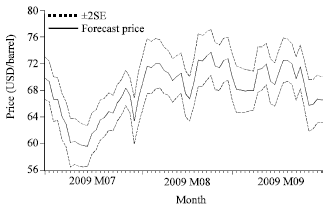
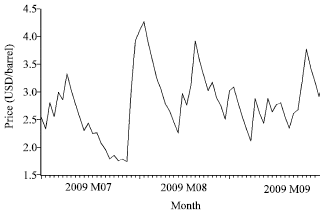
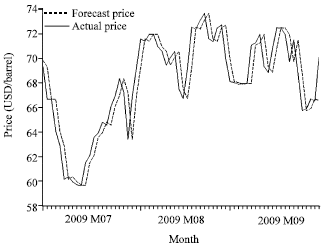
Research Article
A Comparative Study on Box-Jenkins and Garch Models in Forecasting Crude Oil Prices
Faculty of Industrial Sciences and Technology, Universiti Malaysia Pahang, Lebuhraya Tun Razak, 26300 Kuantan, Pahang, Malaysia
Maizah Hura Ahmad
Faculty of Science, Universiti Teknologi Malaysia, 81300 Skudai, Johor, Malaysia
Lee Chee Nian
Faculty of Science, Universiti Teknologi Malaysia, 81300 Skudai, Johor, Malaysia
Noryanti Muhammad
Faculty of Industrial Sciences and Technology, Universiti Malaysia Pahang, Lebuhraya Tun Razak, 26300 Kuantan, Pahang, Malaysia