Research Article
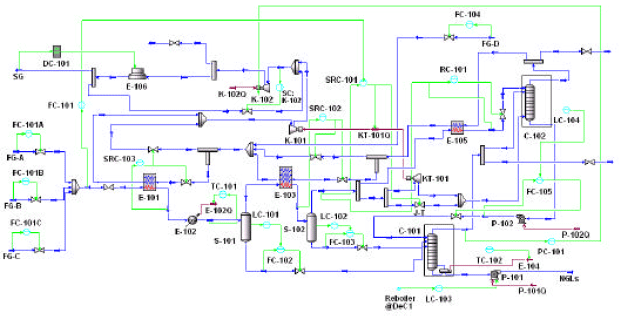
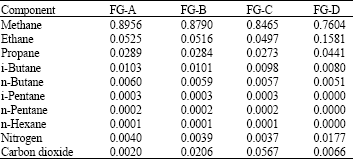
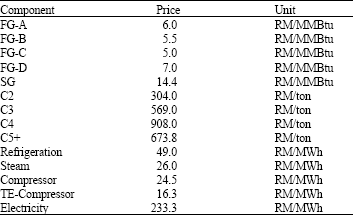
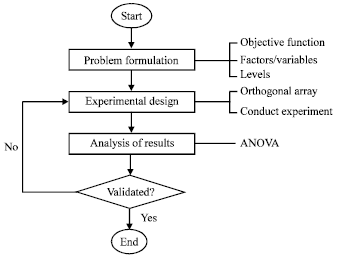
Selection of RGP Optimization Variables using Taguchi Method
Department of Chemical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia
M. Ramasamy
Department of Chemical Engineering, Universiti Teknologi PETRONAS, Bandar Seri Iskandar, 31750 Tronoh, Perak, Malaysia