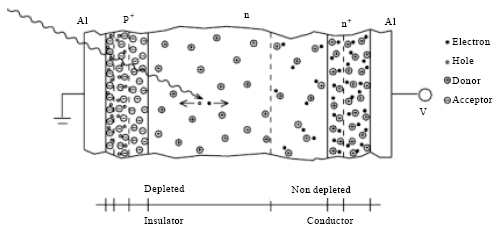
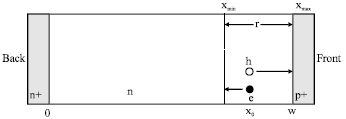
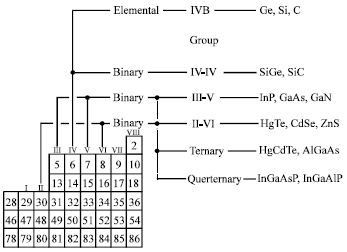
Review Article
Semiconductor Detectors and Principles of Radiation-matter Interaction
Dipartimento di Elettrotecnica ed Elettronica, Politecnico di Bari, V.E. Orabona, 4-70125 Bari, Italy
M. D`Aloia
Dipartimento di Elettrotecnica ed Elettronica, Politecnico di Bari, V.E. Orabona, 4-70125 Bari, Italy
B. Castagnolo
Dipartimento di Elettrotecnica ed Elettronica, Politecnico di Bari, V.E. Orabona, 4-70125 Bari, Italy