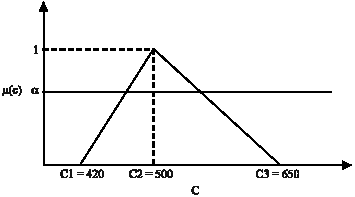
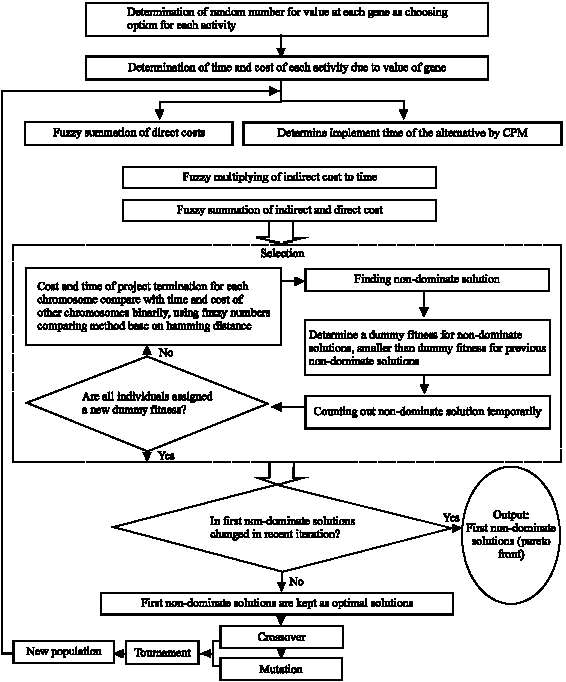
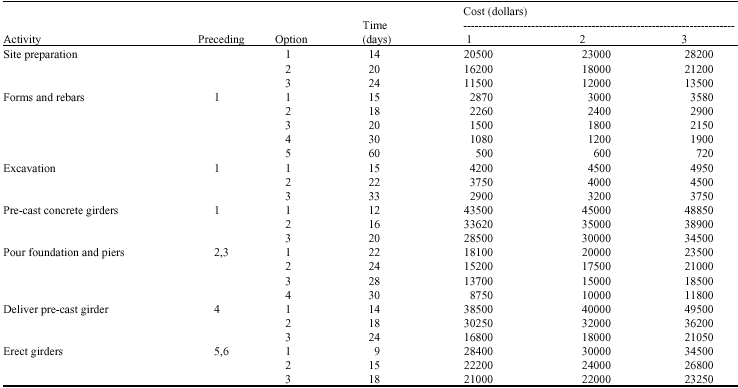
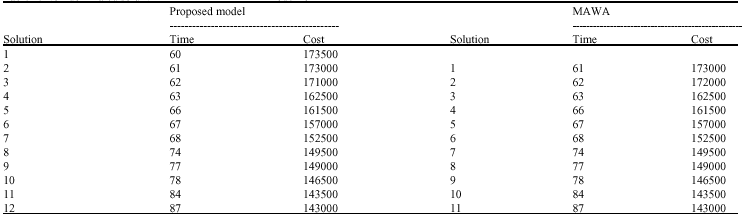
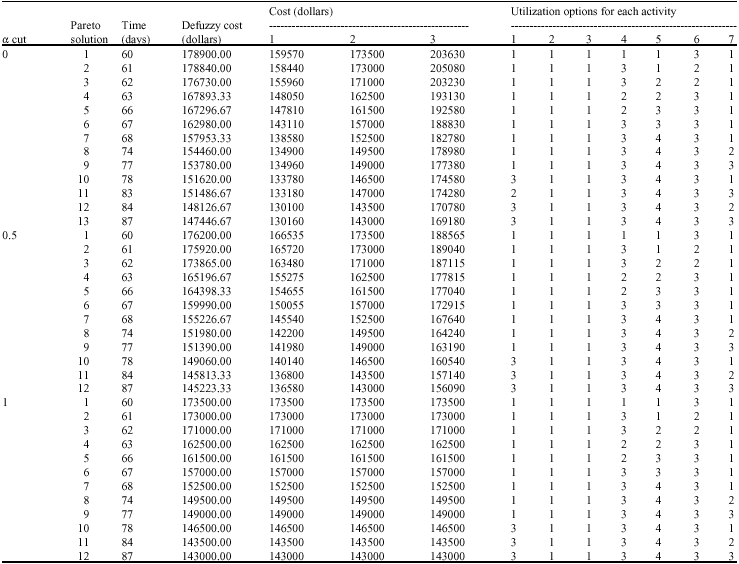
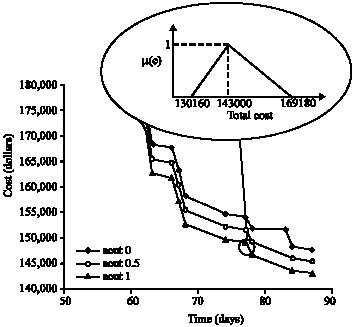
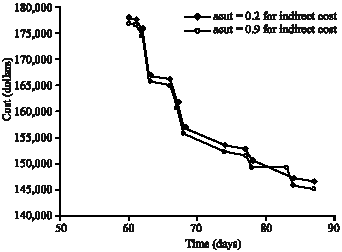
Research Article
Time-Cost Trade-off Problem in Construction Project Management, Based on Fuzzy Logic
Department of Civil Engineering, IUST, Iran
A. Afshar
Department of Civil Engineering, IUST, Iran
E. Eshtehardian
Department of Civil Engineering, IUST, Iran