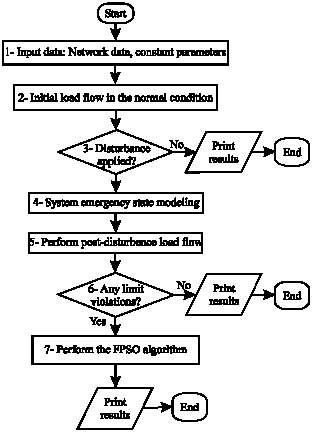
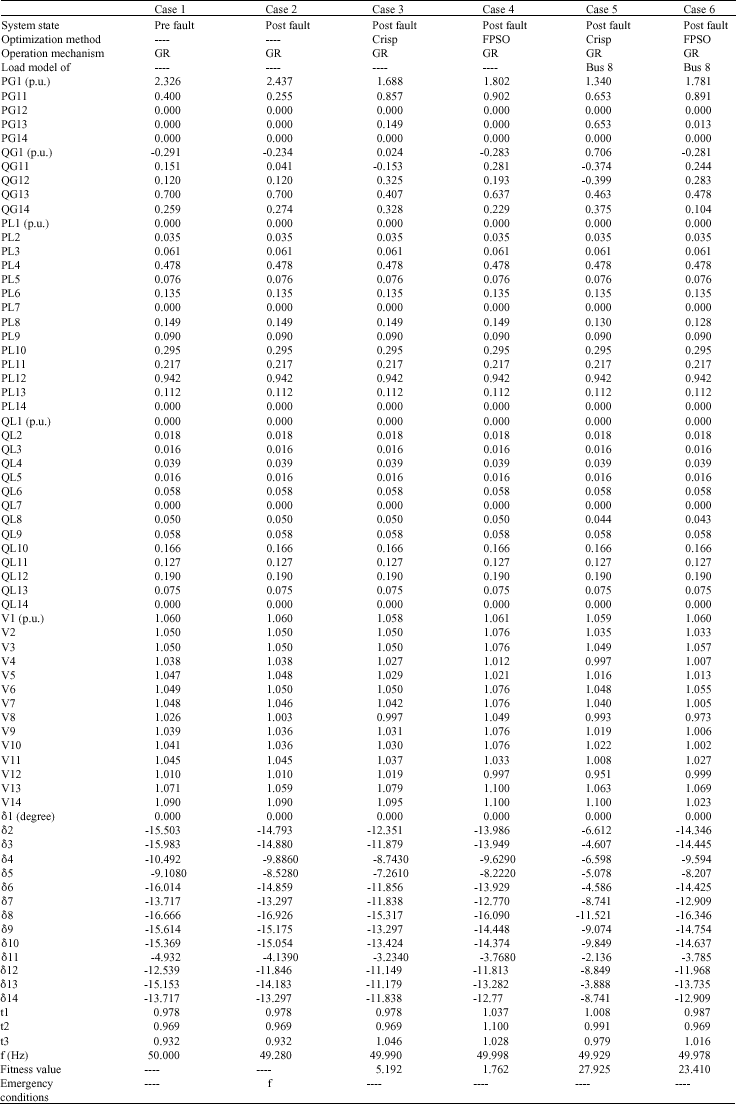
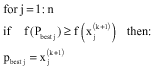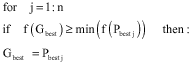Research Article
Optimal Design of Load Shedding and Generation Reallocation in Power Systems Using Fuzzy Particle Swarm Optimization Algorithm
Department of Electrical Engineering, University of Isfahan, Hezar-Jerib St., Postal Code 8174673441, Isfahan, Iran